підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 120. Обчисліть перестановки
1) 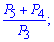
Розв'язання:
Для спрощення Ви повинні знати формулу перестановки 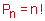
Все решта зводиться до спрощення дробів. Наприклад заданий дріб зводиться до вигляду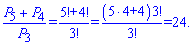
2) 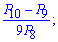
Розв'язання:
Виконуємо перетворення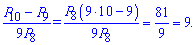
3) 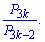
Розв'язання:
Перетвореннями отримаємо не число а формулу
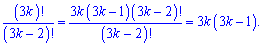
---====================---
Приклад 121. Скількома способами можна скласти список з 5 учнів?
Розв'язання: В подібних прикладах і взагалі в комбінаториці потрібно навчитися вдумуватися у завдання. Так, на першому місці можна поставити одного з п'яти учнів, на другому – одного з чотирьох, оскільки на першому вже хтось стоїть. І таким чином до останнього учня. В результаті список можна скласти 5! способами, тобто є 120 варіантів списків 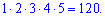
---====================---
Приклад 122. У ліцеї n класів і n класоводів. Скількома способами можна розподілити класне керівництво між учителями?
Розв'язання: Завдання аналогічне попередньому, тільки стосується учителів. Першому класу можна спів ставити одного з n класоводів, другому з n-1 і аж до останнього класу. Остаточно отримаємо, що між учителями можна розподілити класне керівництво n! – способами.
---====================---
Приклад 123. Скільки різних чотирицифрових чисел можна записати з допомогою цифр 0, 2, 4, 6, якщо кожну з них використовувати тільки один раз?
Розв'язання: На перше місце можна поставити одну з трьох цифр – нуль ставити не можна. Далі можна ставити перестановки з трьох інших цифр, оскільки ту що стояла на першому місці двічі використовувати не можна за умовою. Мовою формул це матиме вигляд 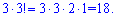 Можна записати 18 різних чисел.
Можна записати 18 різних чисел.
Відповідь:18.
---====================---
Приклад 124. Скільки різних слів можна одержати, переставляючи букви слова:
1) "ліцей";
2) "галушка";
3) "шаровари" (словом вважається будь-яка послідовність літер)?
Розв'язання: Переставляючи означає, що не можна дублювати букви, а лише використовувати наявні. Крім цього Ви повинні знати, що якщо в слові дві однакові букви то кількість перестановок ділиться на 2!, три –3!, оскільки від перестановки двох чи більше однакових букв зміст слова (кількість) не поміняється. На основі цього розв'язуємо завдання.
1) "ліцей"=5 різних букв. Кількість перестановок рівна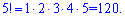
2) "галушка" =в слові 7 букв, буква "а" повторюється 2 рази, отже кількість рівна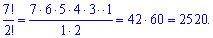
3) "шаровари" = 8 букв, 2 букви " а" , 2 букви "р", тоді кількість визначаємо із залежності 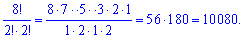
Отримали 10080 різних слів.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Перестановки
- Наступні відповіді - Розміщення
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



