ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 62. Дослідіть функцію та побудуйте її графік:
1) 
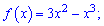
Розв'язання:Перше, що потрібно зробити при дослідженні функції це встановити область визначення.
Для заданого полінома функція визначена на всій дійсній осі D(f)=R.
Другим етапом є перевірка функції на парність, непарність, періодичність.
Оскільки рівність порушується
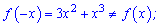
то задана функція ні парна, ні непарна.
Встановлюємо точки перетину з віссю абсцис. Для цього функцію прирівнюємо до нуля
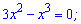
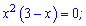
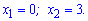
Отримали 2 нулі функції
f(0)=0; f(3)=0.
При рівнянням похідної до нуля знаходимо критичні точки
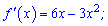
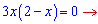
х=0; х=2.
Функція зростає, якщо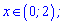 
Спадає на двох ділянках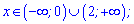
Обчислюємо значення в точках локального екстремуму
f(0)=0; f(2)=12-8=4;
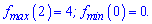
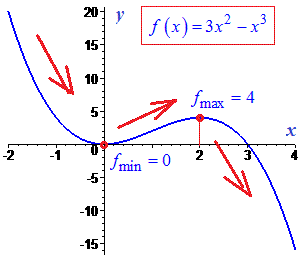
Графік функції матиме наступний вигляд
2) 
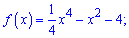
Розв'язання: Областю визначення полінома буде вся дійсна вісь D(f)=R; Перевірка на парність
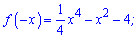
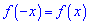- функція парна.
Знаходимо нулі функції, для цього біквадратне рівняння
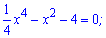
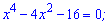
заміною змінних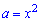 
зводимо до квадратного
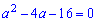
корені якого обчислюємо через дискримінант
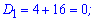
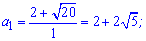
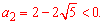
Повертаємося до заміни і розв'язуємо
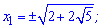
Наступним кроком визначаємо точки екстремуму. Для обчислюємо похідну функції
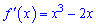
та прирівнюємо її до нуля
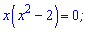
х=0;
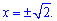
Встановлюємо знаки похідної на проміжках підстановкою, наприклад в одиниці похідна від'ємна
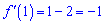
А це значить, що функція на проміжку спадає. На сусідніх ділянках знаки чергуються. Функція спадає, якщо
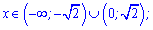
Зростає, якщо
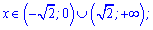
Знаходимо значення функції в точках екстремуму f(0)=-4;
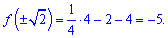
Перша буде локальним максимумом, дві наступні – мінімумом
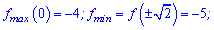
Графік функції зображено на рисунку
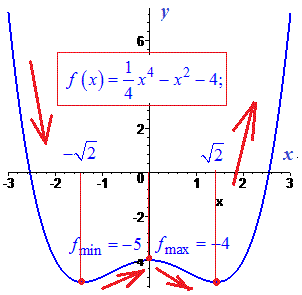
3) 
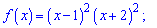
Розв'язання: Задана функція визначена всюди D(f)=R .
З вигляду бачимо, що функція ні парна, ні непарна. Вона перетворюється в нуль при x=1; x=-2.
Визначаємо екстремуми функції. Похідну добутку прирівнюємо до нуля
"
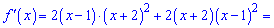
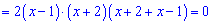та визначаємо критичні точки
x=1; x=-2;
2x=-1; х=-1/2.
Знак похідної визначаємо підстановкою, наприклад в нулі вона від'ємна. Значить функція спадає, якщо змінна належить інтервалу
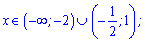
та зростає на решті множини
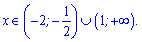
Обчислюємо значення функції в точках екстремуму f(1)=0; f(-2)=0;
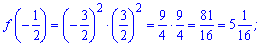
та в нулі f(0)=2*2=4.
Враховуючи знаки похідно, маємо мінімум в двох точках
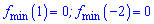
та один максимум
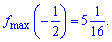
Графік функції із проміжками зростання та спадання зображено нижче
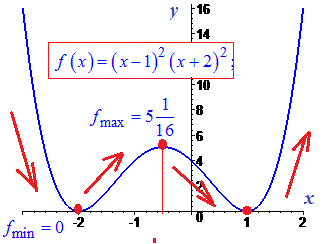
4) 
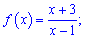
Розв'язання: Дробова функція визначена в усіх точках, окрім нуля знаменника
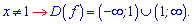
Перевірка на парність показує, що функція ні парна ні непарна
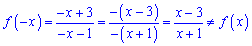
З умови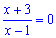 
встановлюємо, що x=-3- нуль функції;
Похідна функції
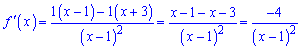
приймає від'ємне значення на всій області визначення, а це означає, що вона всюди спадна Запишемо функцію у вигляді
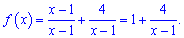
При спрямуванні змінної до безмежності отримаємо вертикальну асимптоту х=1.
Графік функції має вигляд
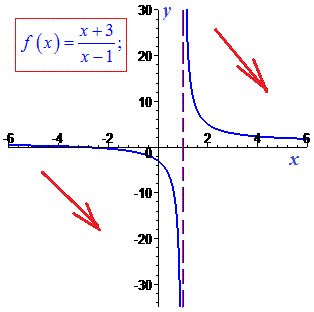
5) 
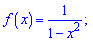
Розв'язання: Облаю визначення буде множина дійсних чисел без двох точок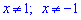 
, які є нулями знаменника.Знайдені точки також будуть вертикальними асимптотами.
Нулів функція не має, це очевидно. Також легко переконатися, що функція парна
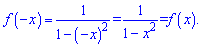
Прирівнявши похідну до нуля
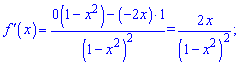
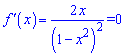
визначаємо екстремум функції х=0; f(0)=1. Справа похідна додатна, а зліва від'ємна. Далі знаки чергуються. Функція спадає на інтервалах
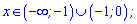
Зростає при наступних значеннях інтервалу
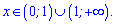
Маємо оду точу максимуму
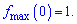
На безмежності функція має горизонтальну асимптоту y=0.
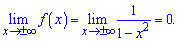
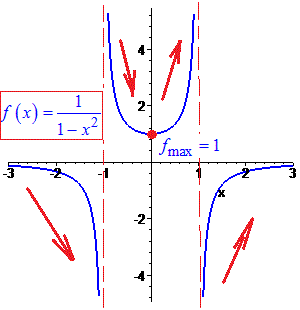
Графік функції зображено нижче
6) 
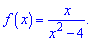
Розв'язання: Нулі знаменника розбивають область визначення на 3 інтервали
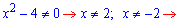
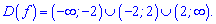
Точка x=0 - нуль функції. Перевірка на парність
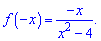
f(-x)=-f(x)- функція непарна. Визначаємо екстремуми через похідну
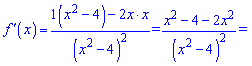
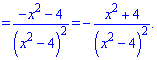
Похідна
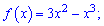
відмінна від нуля, отже робимо висновок, що функція немає екстремальних точок.
Чисельник завжди більший нуля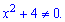 
Отже, функція на всій області визначення спадає. Нулі знаменника х=2 і х=-2 - вертикальні асимптоти.
Графік функції зображено на рисунку
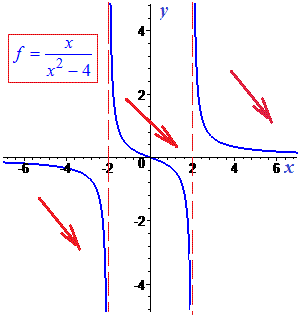
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Найбільше і найменше значення функції на відрізку. №56-61
- Наступні відповіді - Побудова графіків функцій. №63
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
