ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 63. Дослідіть функцію та побудуйте її графік:
1) 
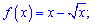
Розв'язання: Область визначення обмежена кореневою функцією
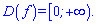
Нулі функції визначаємо із рівняння f(x)=0;
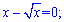
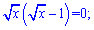
x=0; x=1- розв'язки рівняння.
Критичні точки знаходимо з рівності нулю похідної
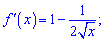
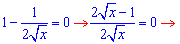
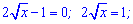4x=1;
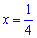- критична точка.
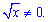
В одиниці похідна додатна
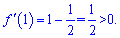
Отже, функція спадає на початку області визначення
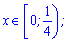
а далі зростає
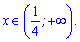
Знайдена критична точка є мінімумом, а функція в ній приймає значення
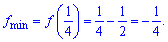
Функція з проміжками зростання та спадання зображена на графіку
2) 
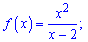
Розв'язання: Виключаємо нулі знаменника з області визначення
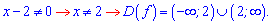
Задана дробова функція f(x)- ні парна, ні непарна, оскільки жодна з умов не виконується
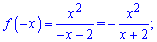
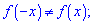
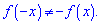
Прирівнявши чисельник до нуля
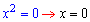
знаходимо нуль функції. Знаходимо точки екстремуму
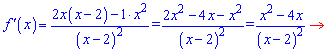
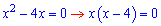
х=0; х=4
та значення функції в точках
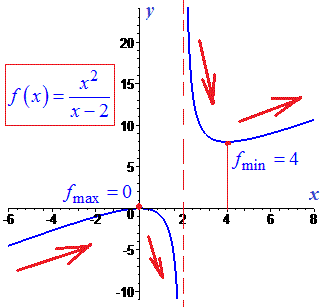
f(0)=0; f(4)=16/2=8.
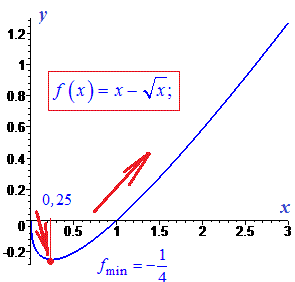
В одиниці похідна від'ємна, отже на цьому проміжку функція спадає. Функція зростає, якщо аргумент належить до інтервалів
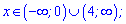
та спадає поза ними
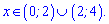
Знайдені критичні точки будуть максимумом та мінімумом з відповідними значеннями функції
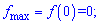
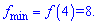
В нулі знаменника функція має вертикальну асимптоту x=2
Графік функції має вигляд
3) 
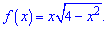
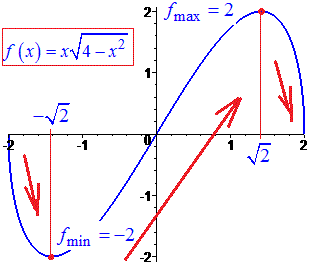
Розв'язання: З умови обмеження на корінь встановлюємо область визначення
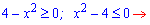
D(f)=[-2;2];
Нулями функції з умови f(x)=0 будуть точки
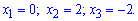
Перевірка на парність
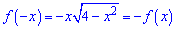
показує, що функція непарна. З рівності нулю похідної визначаємо точки екстремуму
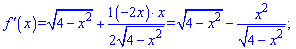
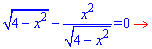
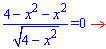
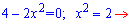
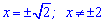
та значення функції
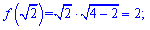
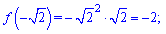
В нулі похідна додатна, отже між екстремумами функція зростає. На лівому краю проміжку маємо мінімум
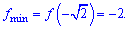
а на правому максимум.
Графік функції має наступний вигляд
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Побудова графіків функцій
- Наступні відповіді - Показникова функція та її властивості
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
