ГДЗ Алгебра 11 клас Мерзляк. Найбільше і найменше значення функції на відрізку. №56-61

ГДЗ Алгебра 11 клас Мерзляк

підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.

1 Варіант

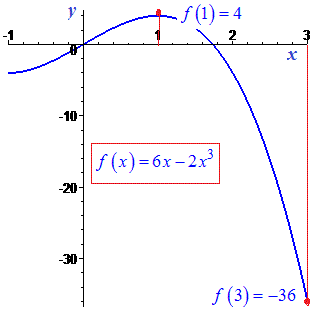
Приклад 56. На яку множину функція 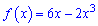відображає відрізок [-1; 3] ?

Розв'язання: В завданні потрібно знайти область значень. Для цього обчислюємо похідну і прирівнюємо її до нуля
похідна функції
умова
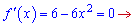
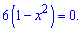
З цієї умови маємо дві критичні точки 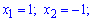які належать проміжку. Обчислюємо значення функції на краях проміжку та в критичних точках
f(1)=4; f(-1)=-4;
f(-1)=-4; f(3)=18-54=-36.
Виписуючи мінімум і максимум функції, дістанемо область значень E(f(x))=[-36;4].
На проміжку функція матиме наступний вигляд
графік функції

Приклад 57. Знайдіть найбільше і найменше значення функції 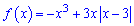на проміжку [0; 4].

Розв'язання: Область визначення функції вся дійсна вісь D(f)=R;
Розкриємо підмодульну функцію і розглянемо її на кожному інтервалі

1) функція
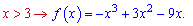
Похідну прирівнюємо до нуля
похідна функції
квадратне рівняння
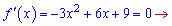
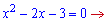
та отримуємо, що критичні точки не належать розглядуваній області (x>3)

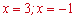
2) функція
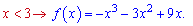
Прирівнюємо похідну до нуля

похідна функції
квадратне рівняння
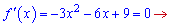
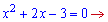
та отримаємо один розв'язок, що належить проміжку
критичні точки
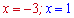
Перевіряємо краї проміжку та знайдену критичну точку
f(0)=0; f(1)=-1-3+9=5; f(4)=-64+12=-52.
Записуємо мінімум і максимум функції

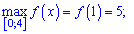
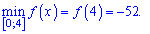
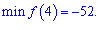
ЇЇ графік має наступний вигляд
графік функції

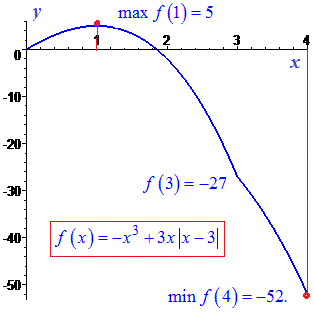
Приклад 58. Подайте число 60 у вигляді суми двох додатних чисел так, щоб сума їх квадратів була найменшою.

Розв'язання: Нехай один доданок х, тоді другий 60 –х, тоді умова набуде вигляду
функція
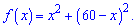
Потрібно знайти максимум функції на проміжку

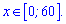
Обчислюємо похідну функції
похідна функції
спрощення
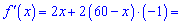
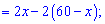
та прирівнюємо її до нуля

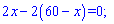
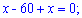
2х=60; х=30.
знаки похідної
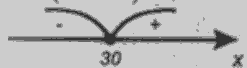
Отримали число x=30, відповідно другий доданок 60-30=30.
Відповідь: 30 і 30.

Приклад 59. Знайдіть додатне число, потроєний квадрат якого більший за подвоєний куб цього числа на найбільше значення.
Розв'язання: Нехай х- додатне число, тоді умова полягає в знаходженні максимуму від виразу 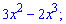функція
Позначимо через функцію 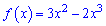та знайдемо її критичну точку
похідна функції

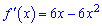
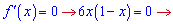
х=0; х=1.

знаки похідної
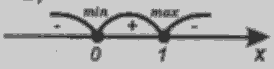
Відповідь: Більшим значенням є х=1.

Приклад 60. Якими мають бути сторони прямокутника, периметр якого дорівнює 60 см, щоб його площа набувала найбільшого значення?

Розв'язання: Нехай х- одна сторона прямокутника, а друга x+a.

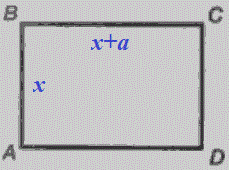
Периметр рівний
2(2х+а)=60 (см);
2х+а=60:2=30 (см);
a=30-2x (см).
x+a=x+30-2x=30-x (см).
Формула площі прямокутника в позначеннях на буде вигляду
S=x*(30-x).
Через похідну знаходимо екстремум площі
S'(x) =30-2x;
30-2x=0; x=15(см).
Знаходимо другу сторону прямокутника
x+a=30-x=30-15=15 (см).
Відповідь: 15 і 15 см.

Приклад 61. У рівнобедрений трикутник, кут при основі якого дорівнює 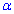, вписано коло радіуса r. Знайдіть площу трикутника. При якому значенні 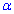площа трикутника буде найменшою?

Розв'язання:

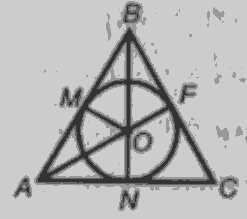
Оскільки трикутник 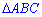- рівнобедрений то кути при основі рівні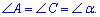
ON=OM=r.
Схема обчислень наступна – потрібно виразити два катети через відомі величини (радіус і кут). Далі дослідити площу на екстремум
Кути рівні половині
кути трикутника

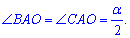
1) 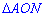- прямокутний. Це дозволяє виразити одну сторону через відомі

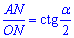
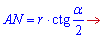
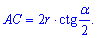
2) Трикутник 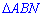- теж прямокутний.
Складаємо співвідношення

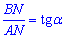
з якого знаходимо другу сторону

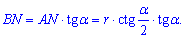
3) Площа трикутника через знайдені сторони запишеться наступним чином

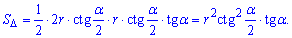
Запишемо функцію як залежність від кута та дослідимо її на екстремум

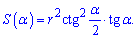
Похідну від площі шукаємо як від добутку складеної функції на просту. Уважно розберіться з обчисленнями, вони достатньо зрозумілі, хоч і складні
похідна

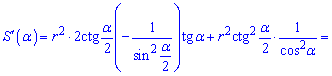
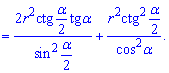
Прирівнюємо похідну до нуля
умова
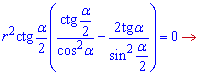
Радіус не може бути нульовим

Решта множників прирівнюємо до нуля

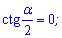
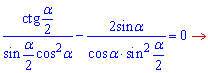
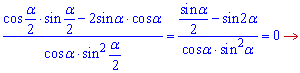
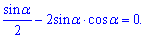
Знаменник повинен бути відмінний від нуля

Чисельник дає такий розв'язок

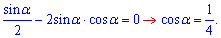
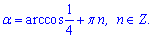
При куті 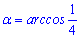площа трикутника буде найменшою.