Знайти напрям та величину градієнта скалярного поля в точці

Нехай задана функція u=f(x;y;z) диференційовна в кожній точці області визначення D.
Побудуємо вектор, проекції якого на осі координат є значення часткових похідних функції u в заданій точці M(x;y;z)Ж

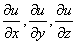
Цей вектор називається градієнтом функції u(x;y;z).
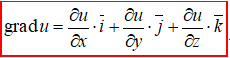(1)
Він спрямований в сторону найбільшого зростання функції u=f(x;y;z) в заданій точці M(x;y;z), а модуль градієнта (довжина) рівний швидкості росту функції в цьому напрямку.
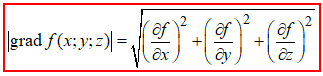(2)
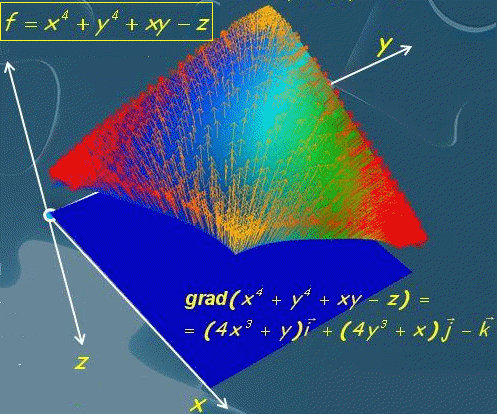
Приклад поля градієнтів наведено нижче


Кут між градієнтами u, v визначається за формулою, як і для кута між векторами:
(3)

Як знайти градієнт поля в точці?

Приклад 2.1 Знайти напрям та величину градієнта поля z=√(x²+y²+6) в точці M(3;1).
Розв'язування: Градієнтом grad(z) функції z(x, y) є вектор, який знаходимо за формулою
(4)
Формули в цьому і всіх наступних завданнях будемо дублювати, щоб Ви їх швидко запам'ятали + не тратили часу на гортання сторінкою вгору - вниз.
Далі дотримуємось простого алгоритму: обчислюємо часткові похідні від z в точці M(3;1)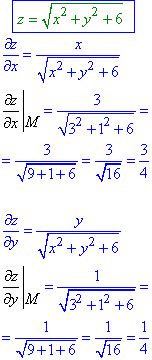

Записуємо за формулою (4) напрям grad(z) поля в точці M: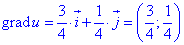

Щоб знайти величину |grad(z)| градієнта поля в точці застосовуємо формулу (3):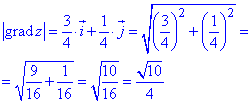


Ось і вся методика розв'язування таких завдань.

Приклад 2.2 В яких точках простору Oxyz градієнт скалярного поля u=x³+y³+z³-3xyz:
а) перпендикулярний до осі Oz;
б) дорівнює нулю?
Розв'язування: Спершу знаходимо часткові похідні функції: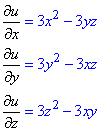

Запишемо напрям градієнта поля grad(u) в точці :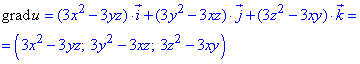

Далі для кожного пункту умови використовуємо властивості градієнта (кутів):

а) Градієнт grad(u) перпендикулярний до осі Oz, якщо скалярний добуток їх напрямних векторів дорівнює нулю.
Напрямний вектор осі Oz:
(0;0;1).
Скалярний добуток напрямних векторів grad(u) і k: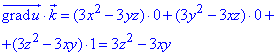

Умова перпендикулярності напрямних векторів grad(u) і k: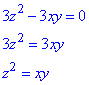

Отже, градієнт grad(u) перпендикулярний до осі Oz у всіх точках поверхні z²=xy.

б) Використаємо результати, отримані на початку.

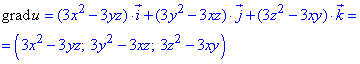
Градієнт grad(u)=0 дорівнює нулю, якщо всі компоненти вектора вище рівні нулю.
Розв'язуємо систему рівнянь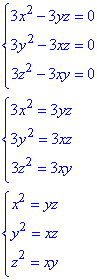

звідси x=y=z.
Це означає, що градієнт grad(u) дорівнює нулю у всіх точках прямої x=y=z.

Як знайти кут між градієнтами полів u, v?

Приклад 3.1 Визначити кут між градієнтами поля
u=x²+y²-z² у точках A(ε;0;0) і B(0;ε;0).
Розв'язування: Тут не задано двох скалярних полів, зате маємо дві точки. Тому спершу знаходимо градієнти в точках, а вже після того кут між ними.
Обчислюємо часткові похідні І порядку в точках A(ε;0;0), B(0;ε;0):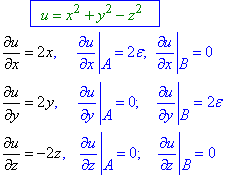

Запишемо напрям градієнта grad(u) поля в точці A: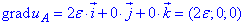

та в точці B: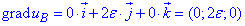

Вже з аналізу компонент градієнтів зрозуміло, що кут між ними 90 градусів.
Але формально повинні обчислити скалярний добуток градієнтів в точках:
2ε·0+0·2ε+0·0=0
Оскільки скалярний добуток дорівнює нулю, то кут між градієнтами у точках A і B прямий, тобто дорівнює 90⁰.

Приклад 3.2 Знайти кут між градієнтами скалярних полів u(x,y,z), v(x,y,z) у точці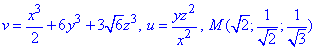

Розв'язування: Градієнтом скалярних полів v, u є вектори: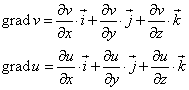

Знайдемо часткові похідні першого порядку в точці M(√2;1/√2;1/√3):

Запишемо напрями градієнтів полів: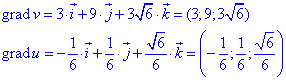

Знайдемо скалярний добуток градієнтів: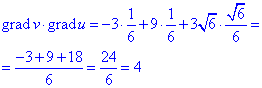

Обчислюємо модулі |grad(v)|, |grad(u)| градієнтів: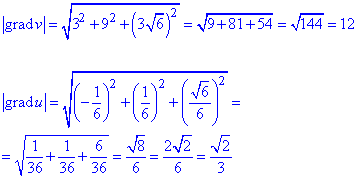

Підставляємо модулі градієнтів та їх скалярний добуток в формулу косинуса кута φ: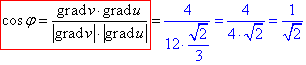

Отримали cos(φ)=√2/2, тому робимо висновок, що кут між градієнтами в точці M рівний φ=45⁰.

На практичних переважно будете отримувати кути кратні 30 або 45 градусів. Рідко який викладач додумається дати завдання в якому після обчислень отримаєте не табличний кут, хоча й таке можливо.
За урок основні формули та терміни розглянули; лишається застановити, щоб не спішили та уважно обчислювали часткові похідні (саме в них нерідко допускаєте помилки), все решта, що тут вчили Вам має бути більш-менш зрозумілим.