Як знайти похідну скалярного поля у точці M у напрямі вектора?

Часткові похідні функції u=f(x;y;z) за змінними x, y, z виражають «швидкість змінення» функції за напрямом координатних осей.
Нехай M(x;y;z) яка-небудь інша точка цієї осі, M0M - довжина відрізку.
Нехай M необмежено наближається до M0. Границя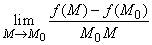

називається похідною від функції f(M) за напрямом 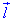(або вздовж осі 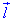) , і позначається: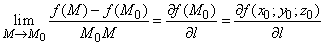

Ця похідна характеризує «швидкість змінення» функції в точці M₀ за напрямом .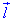
Припустимо тепер, що функція f(x;y;z) має в розглядуваній області неперервні часткові похідні.
Нехай вісь 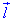утворює з осями координат кути α, β, γ. Тоді
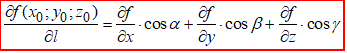(1)
Самі часткові похідні є частковим випадком похідної за напрямом.
В кожній точці області D, в якій задана функція u=f(x;y;z), визначимо вектор, проекціями якого на осі координат є значення часткових похідних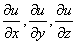

цієї функції у відповідній точці:
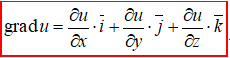(2)

Цей вектор називається градієнтом функції u(x;y;z).
Говорять, що в області D визначено векторне поле градієнтів.
Нехай дано скалярне поле u(x;y;z) і визначено в цьому скалярному полі поле градієнтів

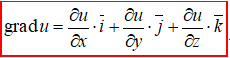
Похідна ∂u/∂s за напрямом деякого вектора 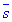дорівнює проекції вектора gradu на вектор .

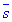Властивості градієнта

А) Похідна в даній точці за напрямом вектора s має найбільше значення, якщо напрям вектора 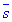співпадає з напрямом градієнта; це найбільше значення похідної дорівнює |grad u|.

Б) Похідна за напрямом вектора, дотичного до поверхні рівня, дорівнює нулю.

Якщо функція u=u(x;y) є функція двох змінних, то вектор grad(u) лежить в площині Oxy;
grad(u) направлений перпендикулярно до лінії рівня u(x;y)=c, що лежить в площині Oxy і проходить через відповідну точку.

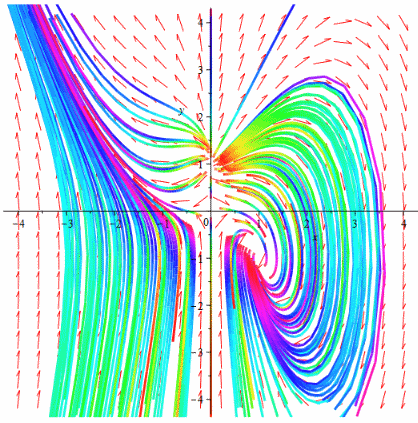
Приклади на похідну скалярного поля u(x, y, z) у точці M у напрямі вектора

Приклад 1.1 Знайти похідну скалярного поля
u=√(x²+y²+z²) у точці M(2,3,6) в напрямку вектора l=i+2j-2k.
Розв'язування: Похідну скалярного поля в точці обчислюють за формулою:
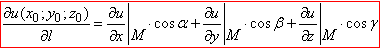(3)
Знайдемо часткові похідні першого порядку в точці M(2;3;6):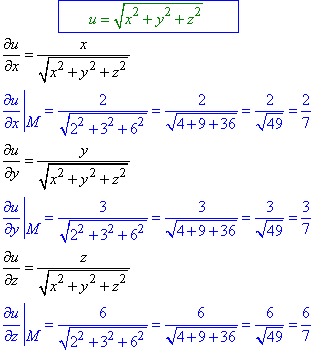

Нехай маємо вектор 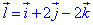, тоді його координати 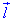(1;2;-2).
Знайдемо напрямні косинуси заданого вектора за формулами: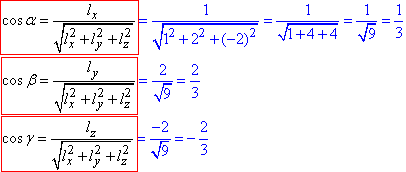

Запишемо похідну 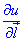за напрямом 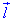(1;2;-2) в точці M(2;3;6):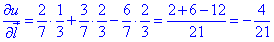

Це весь алгоритм знаходження похідної за напрямом. Повторимо розрахунки на кількох подібних задачах.

Приклад 1.2 Визначити похідну скалярного поля u=x^2yz+arctan(z) в напрямку вектора l=3i+4j в точці M(-1;-1;1).
Розв'язування: Обчислюємо часткові похідні в точці M(-1;-1;1):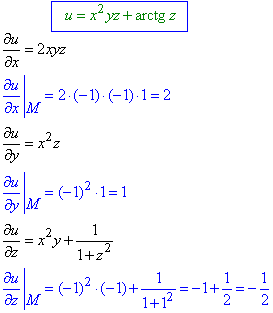

Для вектора 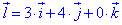запишемо координати (3;4;0).
Обчислюємо напрямні косинуси вектора :

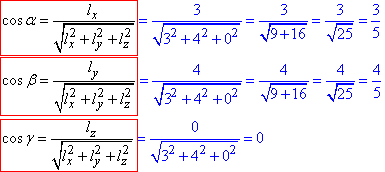
Запишемо похідну ∂u/∂l за напрямом (3;4;0) в точці M(-1;-1;1):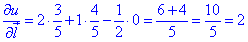

Приклад 1.3 Знайти похідну скалярного поля u=-x+ln(y²+z²) в точці M(2;1;1) у напрямку від даної точки до точки M₁(0;2;2).
Розв'язування: Обчислюємо часткові похідні поля в точці M(2;1;1):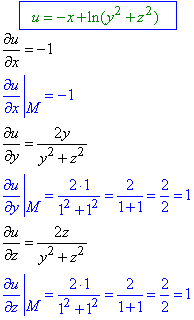

Знайдемо напрям від точки M до M1
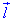=MM₁=M₁(0;2;2)-M(2;1;1)=(-2;1;1)
Знайдемо напрямні косинуси вектора 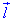(-2;1;1):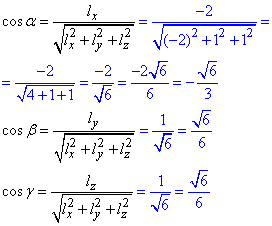

Виписуємо похідну скалярного поля du/dl в точці M за напрямом 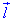(-2;1;1) за формулою:

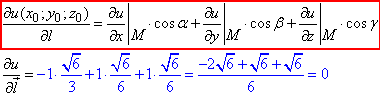
Приклад 1.4 Обчислити похідну скалярного поля u=x^2∙arctg(y)+x∙ln(x+z^2) в напрямку вектора l=6j+2k в точці M(1;3;-3).
Розв'язування: Повторюємо методику обчислення похідної поля за напрямом, для цього шукаємо часткові похідні скалярного поля в точці M(1;3;-3):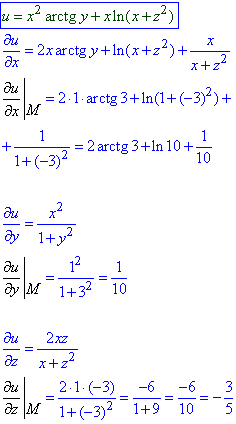

Далі за формулою вектора похідної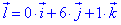

виписуємо координати 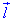(0;6;1) та знаходимо його напрямні косинуси: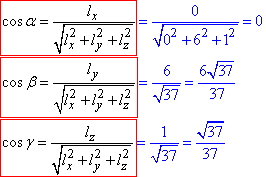

Далі обчислюємо похідну скалярного поля ∂u/∂l за напрямом l(0;6;1) в точці M::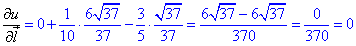

Далі розглянемо, як обчислювати градієнт поля в точці та кут між градієнтами полів.