Якщо функція f(x, y) має в деякому околі точки (a, b) неперервні всі частинні похідні до n+1 порядку включно, то в цьому околі справедлива формула Тейлора:
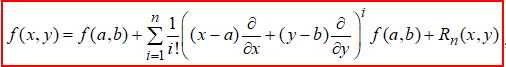
де залишок ряду рівний
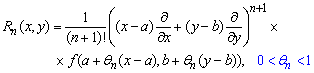
Якщо функція f(x, y) нескінченно диференційовна і границя залишку прямує до нуля при великих номерах
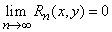
то ця функція допускає представлення у вигляді степеневого ряду Тейлора:
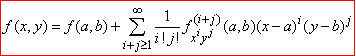 (1)
(1)
Частковий випадок при a=b=0 має назву формули Маклорена
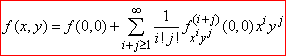 (2)
(2)
Аналогічні формули мають місце і для функції більше ніж двох змінних.
У випадку функцій однієї змінної ряд Маклорена з (2) спрощується до вигляду
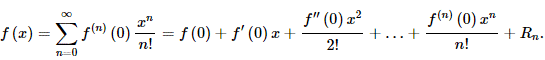 (3)
(3)
Нижче наведена таблиця розкладу в ряд Макларена основних функцій

Її можна застосовувати як для розкладу одномірних функцій, так і коли маємо функцію двох чи більше змінних.
Почнемо вивчення теми з простих прикладів і перейдемо до функцій багатьох змінних.
В найкращому випадку на практиці Вам зададуть розвинути одну з наступних функцій
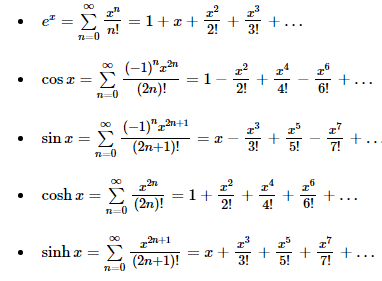
Але на це не дуже розраховуйте та перегляньте, як розкладати в ряд функції виду y(x).
Приклад 1. Розвинути в ряд Маклорена функцію y=cos2(x).
Розв'язування: Спробуйте самостійно знайти похідні функції і підставити в ряд Маклорена (3). Ми ж підемо простішим шляхом, скористаємося тригонометричною тотожністю, яка дозволяє знайти квадрат косинуса через косинус подвійного кута
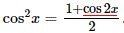
Далі маючи вижче ряд Маклорена для косинуса замінюємо в ньому аргумент з "x" на "2x"
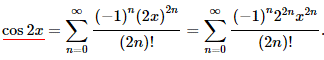
та підставляємо в тільки що виписану формулу:
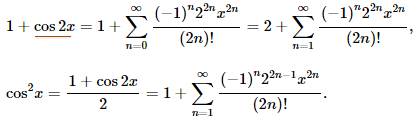
Приклад 2. Розвинути в ряд Маклорена функцію y=exp(k·x).
Розв'язування: Не будемо хитрувати і підставляти замість "х"=2х в готовий ряд експоненти з таблиці, а пройдемо весь шлях обчислень.
Спершу обчислюємо похідні експоненти
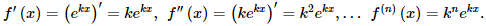
Далі знаходимо значення похідних в 0:
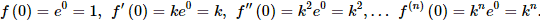
Підставляємо в розклад Маклорена
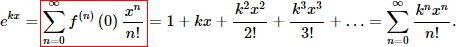
Ось і вся методика розкладу в ряд.
Серед популярних прикладів, які задають наведемо розклад кореневої функції
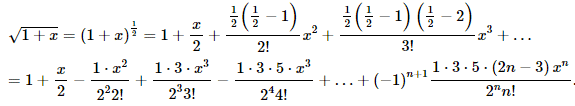
Виводити тут її не будемо, оскільки урок присвячений більше рядам Маклорена для функцій двох змінних.
Як розвинути в ряд Маклорена функцію двох змінних f(x;y)
Приклад 3. Розвинути за формулою Маклорена функцію f(x;y)=ey•cos(x), до третього порядку включно.
Розв'язування: Уважно слідкуйте за алгоритмом дій, оскільки для функцій двох координат обчислень набагато більше.
Спершу обчислюємо значення функції в нулі
f(0,0)=e0*cos(0)=1*1=1.
Наступним кроком знаходимо часткові похідні в нулі.
Обчислюємо часткові похідні першого порядку у точці (0;0): 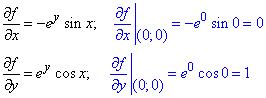
Далі похідні другого порядку в нулі: 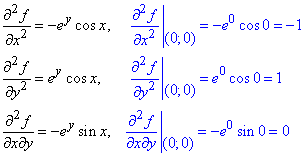
третього порядку: 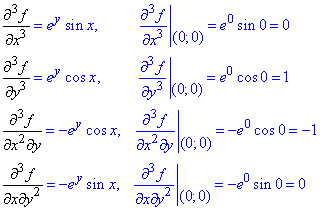
І так далі, скільки вимагають в умові.
Запишемо три перших члени розкладу в ряд Маклорена за формулою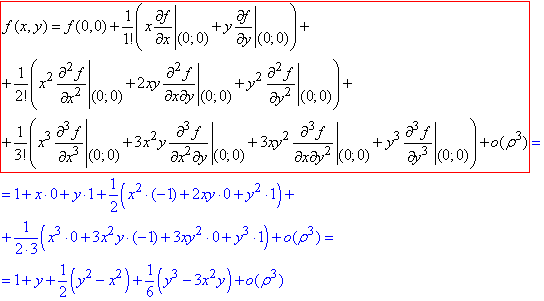
тут і в усіх розкладах ρ=√(x2+y2).
Приклад 4. Розвинути в ряд Маклорена функцію f(x;y)=√(1-x2-y2) до четвертого порядку включно.
Розв'язування: Повторюємо крок за кроком схему розвинення в ряд.
Обчислюємо значення функції в нулі
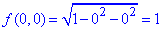
Знайдемо часткові похідні першого порядку в точці (0;0): 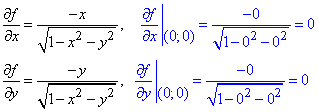
далі часткові похідні другого порядку в нулі: 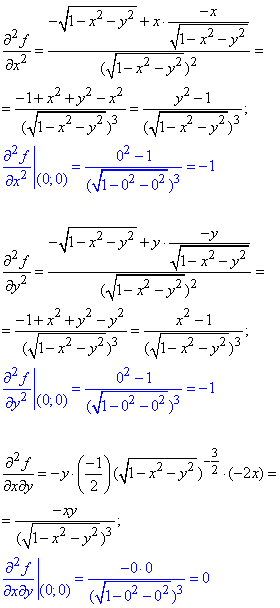
Після цього похідні третього порядку 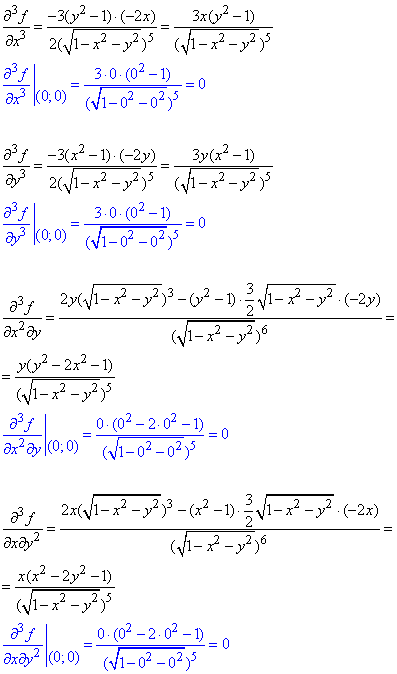
та четвертого порядку в нулі (0;0):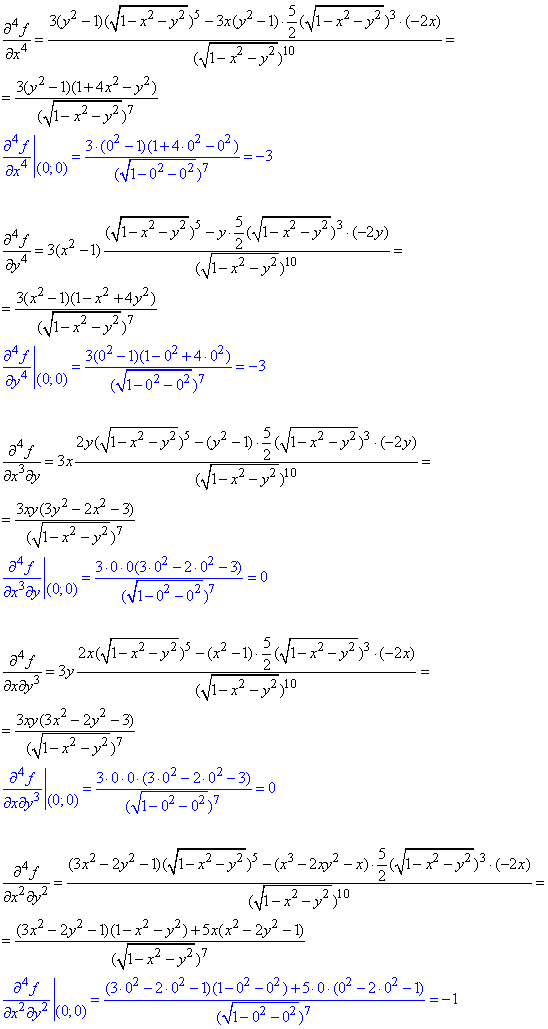
Складаємо ряд Маклорена для функції f(x;y)=√(1-x2-y2) за формулою: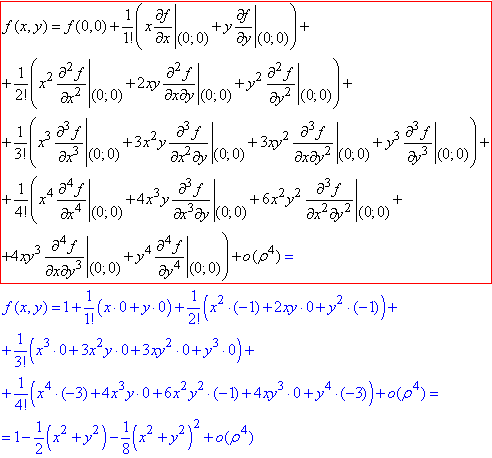
На практиці доводиться оперувати з розвиненнями в ряд складніших функцій, і не до 2 чи 4 порядку, а перших 10, 20, 50 членів розкладу в ряд Маклорена чи Тейлора. Ніхто зараз в ручну виписувати похідні чи шукати рекурентні формули для мішаних чи звичайних частинних похідних не буде. Для того є багато математичних пакетів, окремі з яких заточені тільки на розвинення функцій в ряди.
Покажемо як в пакеті Мейпл розвивати в ряди Тейлора функції:
1) f(x,y)=ln(x+1)*cos(3y) в точці x=1/3, y=Pi/12 перших 4 члени ряду
Розкладемо спершу по "х", після чого по "y"
M1 := series(ln(x+1)*cos(3*y), x = 1/3, 5);
M2 := simplify(series(M1, y = (1/12)*Pi, 5));
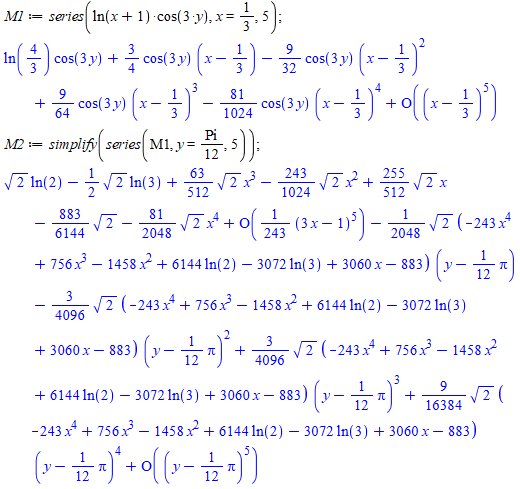
Наведемо 3d рисунок f(x,y) в околі точки x=1/4..1/2, y=0..(1/6)*Pi
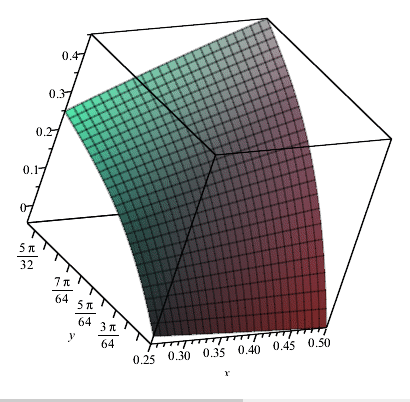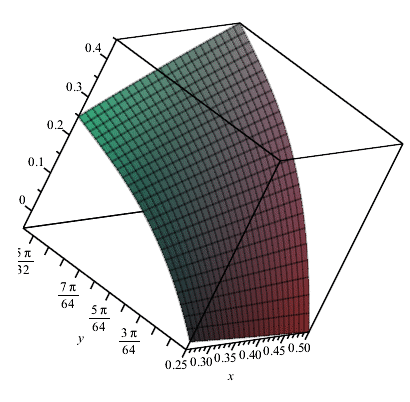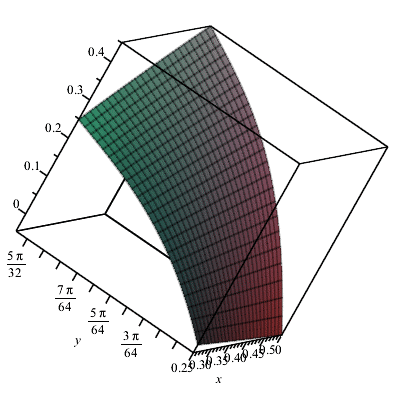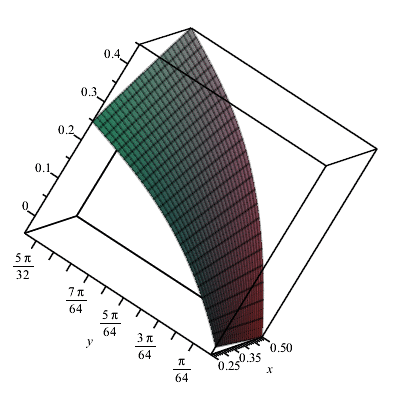
Більше того, в Мейплі можна порівняти графіки розвинення функції в ряд Маклорена з оригіналом, знайти похибку (збіжність) при віддаленні від точки в якій розкладали ряд, а для простих функцій знайти готову формулу розкладу
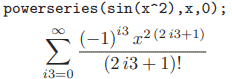
але це вже виходить за межі даного уроку.
Якщо Ви студент, то вчити і знати хоча б один мат. пакет більш ніж необхідно.
Куди б Ви не подалися на роботу – всюди будете мати справу з обчисленнями на комп'ютерах, серед мат пакетів радимо вчити MathCad, Maple, MatLab.

