Повторимо ознаку Діріхле з попередніх уроків і далі перейдемо до розкладу в тригонометричний ряд Фур'є функцій.
Теорема (ознака) Діріхле: якщо функція f(x) періоду 2π кусково-монотонна на проміжку [-π;π] і має в ньому не більше, ніж скінченну кількість точок розриву (першого роду), то її ряд Фур'є збігається до суми f(x0) у кожній точці неперервності й до суми
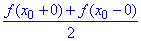
у кожній точці розриву.
(Збірник задач Л. Д. Кудрявцев та інші)
Приклад 8 Розвинути функцію f(x)=π+x, -π≤x≤πв тригонометричний ряд Фур'є та знайти суму ряду в точці x0=π.
Розв'язування: Бачимо, що функція ні парна ні непарна на заданому інтервалі, тому потрібно обчислити усі коефіцієнти ряду Фур'є:
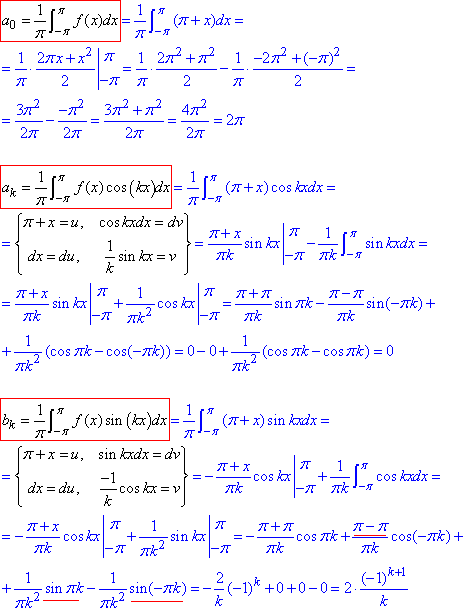
Записуємо ряд Фур'є для функції f(x)=π+x:
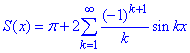
2) Далі читайте уважно, оскільки наведені пояснення є алгортмом відшукання значення суми ряду в точці.
А це Вам потрібно знати, оскільки функція, що задає ряд може мати розриви, а сам ряд визначений в точці розриву.
Ряд збігається до f(x) на –π<x<π.
Сума S(x) отриманого ряду має розрив І роду у точці x0=Pi, є періодичною з періодом 2Pi, тобто S(x)=S(x)+2Pi, тому за теоремою Діріхле отримаємо
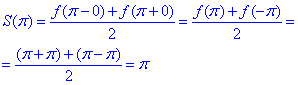
Добре засвоюються уроки в яких багато прикладів, тому розберемо подібне за умовою завдання.
Приклад 11. Розкласти в ряд Фур'є функцію
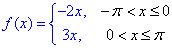
та знайти суму ряду в точці x0=Pi .
Розв'язування: Задана функція ні парна ні непарна, тому використовуємо загальну формулу коефіцієнтів Фур'є:
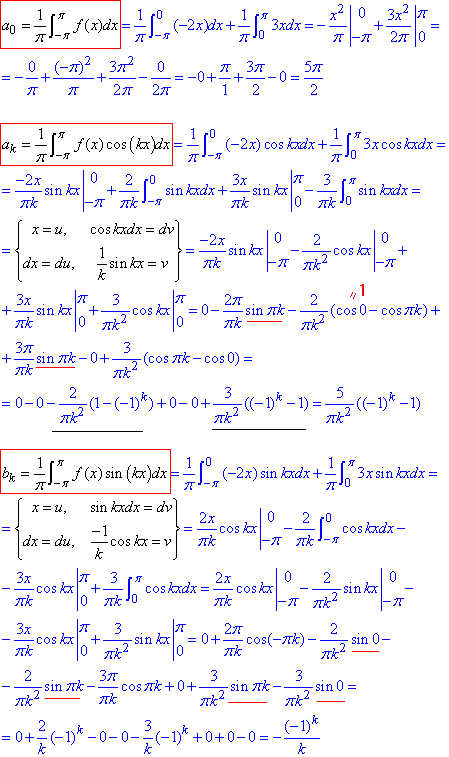
Уважно перегляньте, як тут інтегрували частинами.
Виписуємо для заданої функції ряд Фур'є:
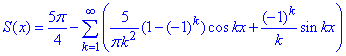
він збігається до f(x) на –π.
2) Сума S(x) ряду має розрив І роду у точці x0=π і є періодичною з періодом 2π, тобто S(x)=S(x+2π), тому за теоремою Діріхле отримаємо
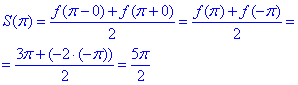
Про те, що f(x) є розривною легко догадатися з аналізу значень функції
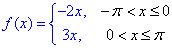
на краях проміжку.
Якщо значення на краях співпадають, то стрибка на графіку ряд не має.
Наведена кількість готових прикладів на розклад в ряди Фур'є функцій допоможе Вам на практичних, можливо для частини з Вас стане довідником в онлайн навчанні.
Вивчайте інтегрування частинами та інтеграли тригонометричних функцій. В прикладах наведено чимало готових формул як це робити, решта – це наполеглива праця над собою та бажання опанувати тему, що вивчаємо!

