На уроці розберемо готові приклади на інтеграл та перетворення Фур'є, навчимося обчислювати відповідні для цього інтеграли.
Але спершу трохи теорії, щоб було загальне понятття, що вчимо та для чого.
Вираз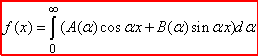 
(1) називається інтегралом Фур'є, де
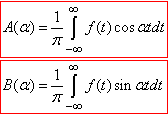(2)
Якщо функція f(x) парна, то інтеграл Фур'є має розвинення лише за косинусами
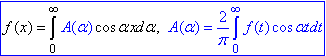(3)
Якщо функція f(x) непарна, то в інтегралі Фур'є присутній розклад лише за синусами
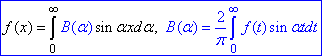(4)
Комплексна форма інтегралу Фур'є має вигляд
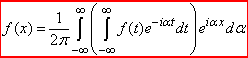(5)
Функцію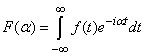 
називають перетворенням Фур'є функції f(x), а |F(α)| - амплітудним спектром.
Де застосовують перетворення Фур'є?:
необхідні для вирішення багатьох прикладних задач, зокрема, мають широке застосування в задачах математичної фізики, електротехніки, радіотехніки, акустики, гідро- і радіолокації, цифрової обробки сигналів, розпізнавання образів і ..
Тут не будемо розбирати умови зображення функції інтегралом Фур’є, вивчати теорме Діні, Ліпшиця і ряд других, це все Ви зможете знайти в додатковій літературі до серії уроків на ряди. Ми хочемо навчити Вас обчислювати перетворення Фур'є, тому далі піде тільки практика.
Алгоритм обчислення інтегралів та перетворень Фур'є
Приклад 1.Зобразити за допомогою інтеграла Фур'є наступні функції.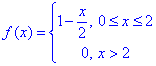 
Розв'язування: Обчислимо коефіцієнти в інтегралі Фур'є
Підставляємо в формулу (1) інтегралу Фур'є: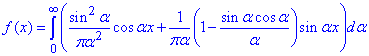 
Поступово від простих прикладів перейдемо до важчих в плані обчислення інтегралів.
Приклад 2. (445) Зобразити за допомогою інтегралу Фур'є такі функції:
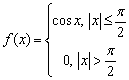
Розв'язування:Функція f(x) кусково-неперервна на заданому інтервалі, тому для неї існує інтеграл Фур'є.
Інтегруванням за (3) ф-лою знаходимо коефіцієнт A(α )
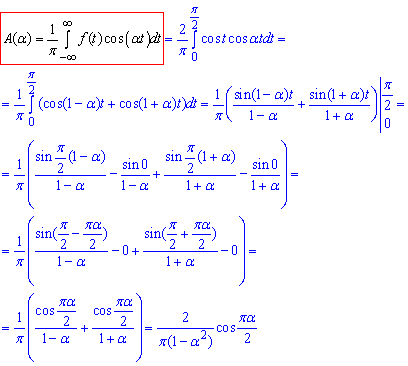
B(α)=0, оскільки задана функція f(x) парна.
Складаємоформулу інтегралу Фур'є:
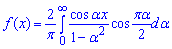
Приклад 3.Зобразити інтегралом Фур'є функцію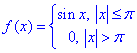
Розв'язування:Почнемо з огляду функції на парність непарність.
A(α)=0, оскільки бачимо, що функція f(x) непарна.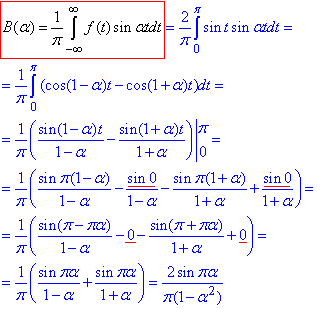 
Підставляємо в інтеграл Фур'є: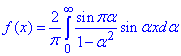 
Розглянемо кілька завдань, де з інтегралу Фур'є при певній заміні змінних слід знайти значення заданого в умові інтегралу.
Приклад 4.Обчислити інтеграл Фур'є функції
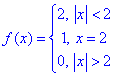та знайти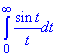 
Розв'язування:Функція f кусково-стала, абсолютно інтегровні на R , також парна на вказаному інтервалі.
Тому за властивістю інтеграла Фур'є в формулі (1) B(α)=0, тоді як A(α)=0 можемо обчислювати за формулою (3):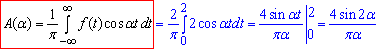 
Підставляємо в інтеграл Фур'є:
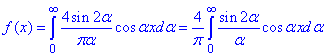(6)
2) Щоб знайти потрібний в умові інтеграл
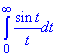
в тільки-що знайденому інтегралі Фур'є (6) виконаємо заміну змінних α=t/2 і x=0, причому f(0)=2 (з умови).
В результаті перетворень отримаємо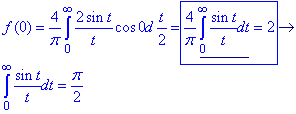 
Приклад 5. (439) Зобразити за допомогою інтеграла Фур'є такі функції:
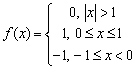
та обчислити
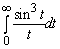
Розв'язування: Обчислюємо A(α):
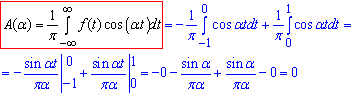
A(α)=0, оскільки функція f(x) непарна.
Наведених обчислень можна було не виконувати. Але для цього, перш ніж інтегрувати, потрібно перевіряти функцію на парність непарністью
Знаходимо B(α):
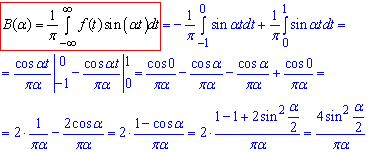
Підставляємо коефіцієнт B(α) в інтеграл Фур'є (1):
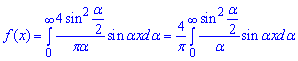
2) Виразимо шуканий в умові інтеграл
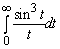
Його можна отримати з інтегралу Фур'є (1):
Зробивши заміну α=2t і x=1/2, причому f(1/2)=1, отримаємо
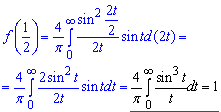
, звідси
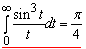
Комплексна форма інтегралу Фур’є
Приклад 7. (453) Обчислити інтеграл Фур'є
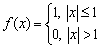
(у комплексній формі).
Розв'язування: Функція f(x) кусково-стала та інтегровна на області в якій задана.
Тому для неї існує інтеграл Фур'є
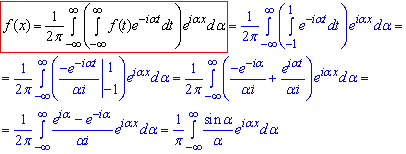
В такому вигляді обчислення завершують.
Синус та косинус перетворення Фур'є винесли окремим уроком, який іде після цього, щоб показати більше готових прикладів по темі.
