Нехай f(x) – абсолютно інтегровна на множині дйсних чисел R , тоді інтеграл
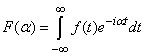
називають перетворенням Фур'є функції f(x).
Інтеграл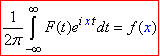 
називають оберненим перетворенням Фур'є функції f(x).
Функцію f(x) називається оригіналом, а F(t) її Фур'є- образом або зображенням.
Функцію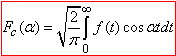 
називають прямим косинус-перетворенням для f(x), а
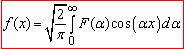– оберненим косинус-перетворенням.
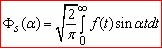– синус-перетворенням функції f(x), тоді як зворотнє
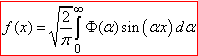– оберненим синус-перетворенням функції
В деяких довідниках пряме синус та косинус-перетворення вводиться з множником перед інтегралом 2/π, а оберене з 1.
На попередньому уроці розібралт чимало прикладів на інтегральну та комплексну форму перетворення Фур'є, далі на уроці розберемо готові приклади на синус та косинус-перетворення Фур'є.
Приклад 8. Знайти косинус та синус-перетворення функцій.
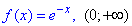
Розв'язування: Перегляньте інтеграли при обчисленні косинус-перетворення Фур'є: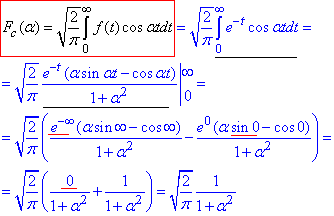 
Тут використовували результати інтегрування частинами, які дальше приведені в цьому завданні. Вони не Важкі і Ви їх повинні знати, оскільки неодноразово зустрічатимете при розв'язування аналогічних завдань.
Далі обчислюємо синус-перетворення Фур'є: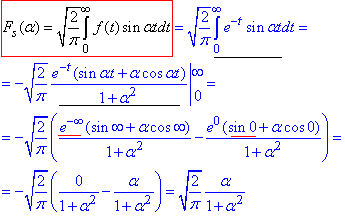 
Покажемо як інтегрували частинами експоненти помножені окремо на косинуси, та синуси.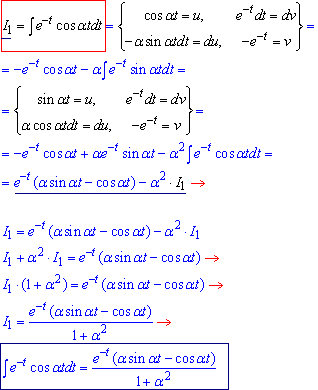 
Синус перетворення Фур'є
Вираз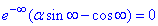 
як добуток нескінченно малої функції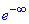 
на обмежену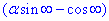 
, аналогічно і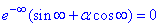 
у сенсі границі інтегральної суми для невластивого інтегралу.
Приклад 9.Обчислити косинус та синус-перетворення функції.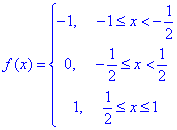 
Розв'язування: Знайдемо косинус-перетворення Фур'є: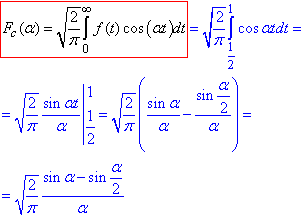 
Проінтегруємо та запишемо синус-перетворення Фур'є:
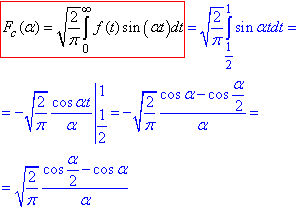
(збірник задач за ред. В. П. Дубовика, І. І. Юрика)
Приклад 10 (453) Обчислити синус та косинус-перетворення Фур'є:
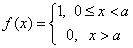
Розв'язування: Домножуємо функцію на косинус та інтегруємо на інтервалі де вона відмінна від нуля за формулою:
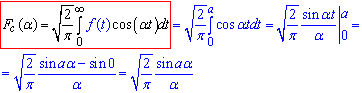
Далі обчислюємо синус-перетворення Фур'є:
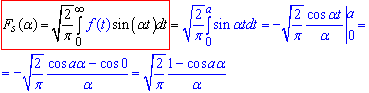
На цьому завдання розв'язано.
Думаю після такої кількості готових прикладів Ви не тільки знатимете , як знайти синус чи косинус-перетворення, а й самі зможете розібратися в подібних завданнях чи проконсультувати друзів.
Приклад 11 (452) Знайти косинус- та синус-перетворення функцій.
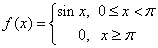
Розв'язування: Знайдемо косинус-перетворення Фур'є:
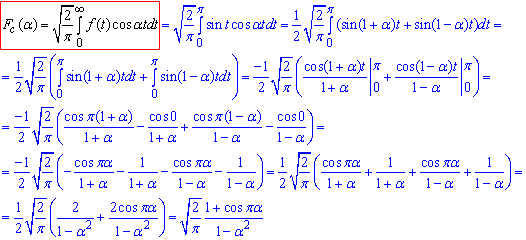
Знайдемо синус-перетворення Фур'є:
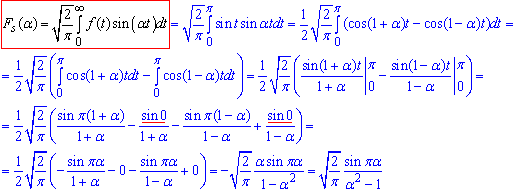
Зважаючи, що синус в нулі рівний нулю та періодичність синуса, отримали компактні кінцеві формули.
Ви повинні добре володіти знаннями з тригонометрії, щоб вільно спрощувати періодичні функції, що отримуєте інтегруванням та знати їх значення.
