Тригонометричний ряд Фурє на [-Pi;Pi]. Побудова графіка суми ряду

Запам'ятайте формулу для розкладу в тригонометричний ряд Фур'є функції на проміжку[-Pi;Pi]
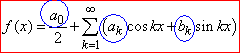(1)
a₀,a_k,b_k - коефіцієнти Фур'є:
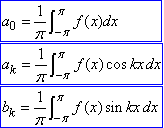(2)
З формул бачимо, що період функції рівний 2π.

Теорема 1. Якщо функція f(x) парна на проміжку (-Pi;Pi), то коефіцієти Фур'є знаходять за формулою
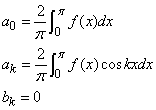(3)
Теорема 2. Якщо функція f(x) непарна на проміжку (-π;π), то всі a_k=0, коеф. b_k обчислюють за правилом:
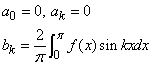(4)

Розклад в ряд Фур'є функції на проміжку (-π;π]

Приклад 18. Розвинути в ряд Фур'є функцію f(x)=x-π на (-π;π]. Накреслити графік суми ряду.
Розв'язування: Пройдемося по алгоритму, який вивчали на попередніх уроках.
Спершу визначимо коефіцієнти Фур'є інтегруванням:

Більшість завдань Вам доведеться інтегрувати частинами, тому добре перегляньте і цю тему.
Далі підставляємо коефцієнти Фур'є в тригонометричний ряд (1):

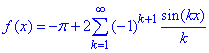
Оскільки функція лінійна, то побудувати графік суми ряду S(x) не важко

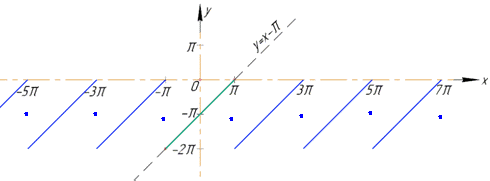
не забувайте, що в точках розриву значення функції за теоремою Діріхле рівне половині стрибка.
Хто цікавиться дослідженням збіжності рядів та вивченням математичних пакетів можемо навчити команд пакету Мейпл
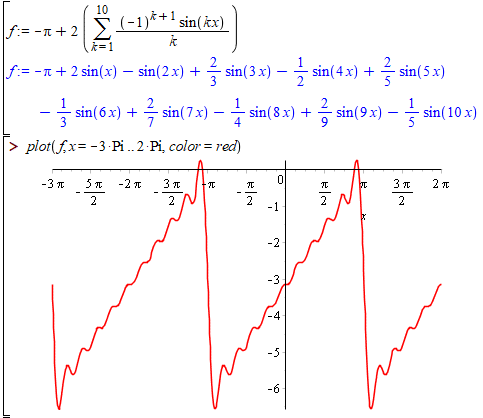
f := -Pi+2*(sum((-1)^(k+1 )/(k)*sin(k*x), k = 1 .. 10));
plot(f, x = -3*Pi .. 2*Pi)
Графік перших 10 членів ряду має вигляд

Приклад 19. Склясти тригонометричний ряд Фур'є функції:

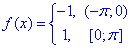
та знайти суму числового ряду

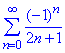
Розв'язування: Тут задано новий тип прикладів де крім тригонометричного ряду Фур'є функції слід додатково встановити суму окремого ряду. Для цього потрібно або скористатися ознакою Діріхле або з графіка вибрати таку точку, в якій ряд із синусів (косинусів) буде змінюватися за законом {(-1)^t}.
Спершу обчислюємо коефіцієнти розкладу. Оскільки f(x) непарна на проміжку (-π;π), то a₀=0 й a_k=0, через інтеграл знаходимо b_k:

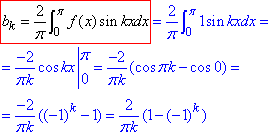
Складаємо тригонометричний ряд Фур'є для заданої функції:
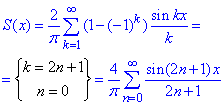(5)
Уважно розберіть момент підстановки n=2k+1, такий прийом доволі часто застосовують, щоб позбутися в ряді множників вигляду (1-(-1)^k).
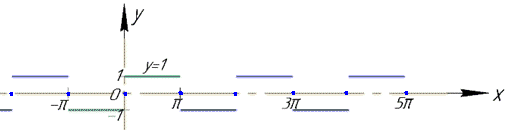
Будуємо графік ф-ї та суми 20 членів ряду S(x) в Мейпл



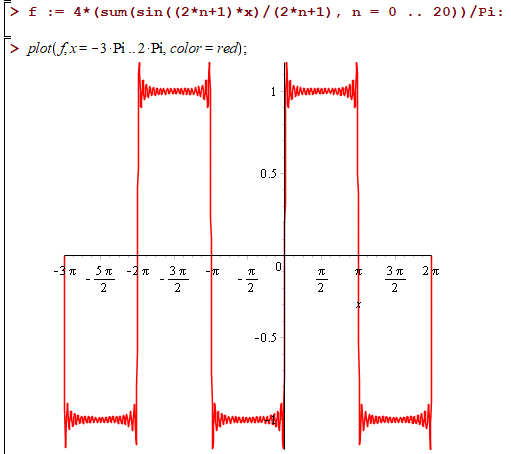
Першу частину завдання ми виконали, залишилося знайти суму числового ряду
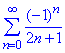(6)
Аналізуючи розклад в ряд Фур'є (5) замічаємо, що точці x=π/2 сума знайденого ряду S(x) має пропорційні доданки до шуканого ряду (6)

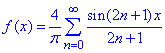
Оскільки f(π/2)=1 (див. графік), то отримаємо

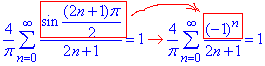
звідси виражаємо шукану суму ряду

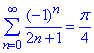
Ось і вся методика розв'язування такого типу завдань.

Приклад 20Розвинути в ряд Фур'є функцію f(x)=x² на проміжку:
а) (-π;π];
б) (0;2π].
Користуючись здобутим результатом, знайти суму рядів

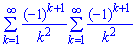
Побудувати графіки рядів Фур'є.
Розв'язування: а) Оскільки функція f(x)=x² парна на проміжку (-π;π), тому коефіцієнти знаходимо з наступних інтегралів:


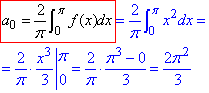
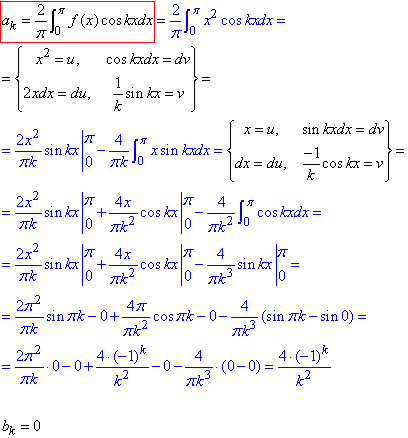
Складаємо розвиненняня функції на проміжку (-π;π] в ряд Фур'є:

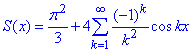
2) Знайдемо суму числового ряду

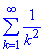
Запишемо розклад досліджуваної функції в ряд
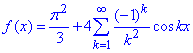(7)
Щоб отримати шуканий ряд з f(x) потрібно, щоб під сумою в чисельнику була одиниця, а це можливо, якщо
(-1)^k*cos(kx)=1.
Це досягається в багатьох точках, зокрема в точці x=π.
Значення функції з початкової умови f(π)=π² (преревірте).
Підставляємо в (7)

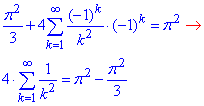
звідси отримаємо потрібну суму ряду

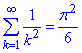
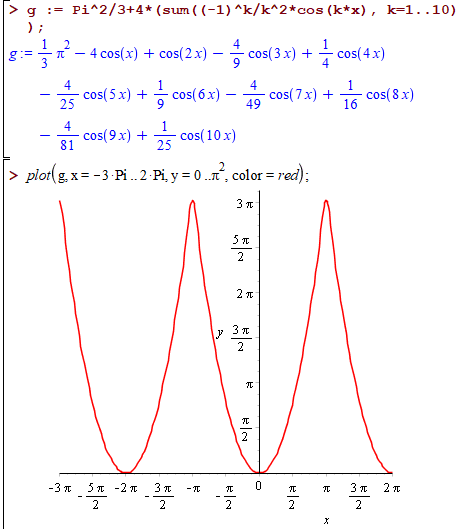
Побудуємо графік суми 10 членів ряду в Мейплі
g := Pi^2/3+4*(sum((-1)^k/k^2*cos(k*x), k=1..10));
plot(g, x = -3*Pi .. 2*Pi, y = 0 .. Pi^2, color = red);

Розв'язування: б) Слід зауважити, що функція f(x)=x² не є парною на проміжку (0;2π].
За парністю, непарністю ф-й на заданих проміжках Ви повинні постійно слідкувати, інакше обчислите інтеграли правильно, але результат Вам не зарахують через те, що інтеграли взяті не ті і з відповіддю не сходиться.
Тому тут потрібно брати усі інтеграли з розкладу Фур'є (2)

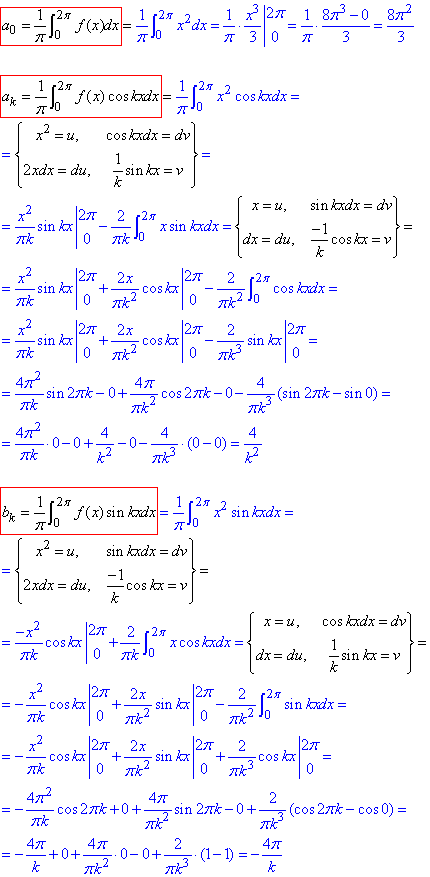
Повторіть правило заміни змінних під інтегралом, воно пригодиться всюди де функція має вигляд f=a·x+b і старше.
Записуємо за формулою (1) тригонометричний ряд Фур'є на проміжку (0;2π]:
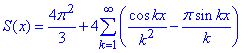(8)
Не забуваємо, що це тільки половина, з того що потрібно знайти в пункті б).
2) Щоб знайти суму числового ряду 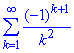потрібно у (8) отримати такі ж доданки під знаком суми,
а для цього потрібно позбутися синусів в розкладі

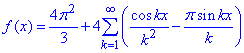(9)
З умови sin(kx)=0 знаходимо точку x=π.
При підстановці в умову f(x)=x² дістанемо f(π)=π², а ряд (9) розпишемо:

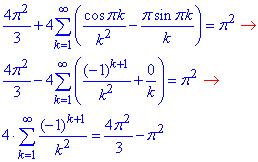
звідси отримаємо шукану суму числового ряду

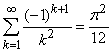
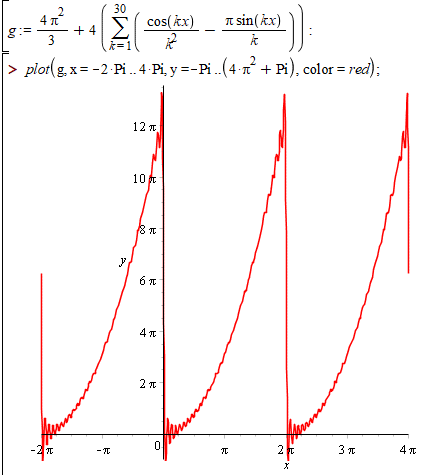
Наостанок побудуємо перших 30 членів ряду (9) в Мейплі
g := 4*Pi^2/3+4*(sum(cos(k*x)/k^2-Pi*sin(k*x)/k, k = 1 .. 30)):
plot(g, x = -2*Pi .. 4*Pi, y = -Pi .. 4*Pi^2+Pi, color = red)

Далі розберемо нові завдання, навчимося розкладати періодичні функції та використовувати комплексну форму ряду Фур’є.