Розклад в ряди Фур'є за косинусами та синусами

Сьогодні розберемо готові приклади в яких функція задана на одній частині інтервалу, а потрібно продовжити на іншу частину так, щоб функція була парною або непарною. В такому випадку маємо справу з довизначенням функції, а самі розвинення в ряд Фур'є йдуть або за синусами або за косинусами. Ось чому і така назва уроку.
Повторимо формули розкладу в ряд Фур'є функції f(x)
(1)
туте a₀,a_k,b_k - коефіцієнти Фур'є:
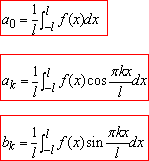(2)

Приклад 15. Розкласти в ряд Фур'є функцію F(x)=1-x на (0;1] по косинусах. Побудувати суму ряду.
Розв'язування: Продовжимо функцію f(x)=1-x на проміжок (-1;0] таким чином, щоб вона була парною.
Для цього вона повинна бути наступною
f(x)=1-|x|.
Ви повинні добре розуміти, як відобразити функцію відносно початку координат, щоб вона стала парною або непарною при такому типі завдань.
Знаходимо a₀

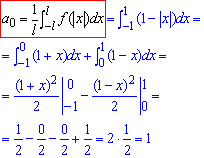
або за властивістю парної функції (див. попередні уроки)

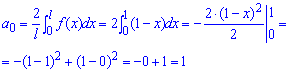
Далі коефцієнти при косинусах для парної ф-ї

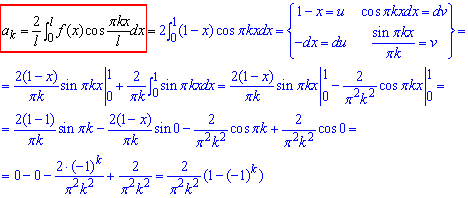
усі b_k=0, оскільки ф-я парна на (-1;1].
Складаємо ряд Фур'є для f(x):

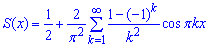
Графік суми ряду S(x)

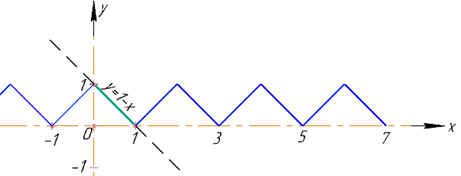
Побудуємо графік перших 10 членів ряду в Мейплі
restart; with(plots):
f := 1/2+2*(sum((1-(-1)^k)/k^2*cos(Pi*k*x), k = 1 .. 10))/Pi^2;
plot(f, x = -2 .. 3, color = red);

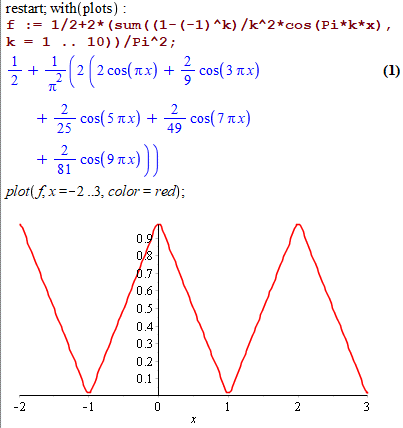
Отримали задовільну збіжність ряду + перевірили, що розклад в ряд виконано правильно.

Приклад 16. Розвинути в ряд Фур'є функцію f(x)=x(2-x) на (0;2] по синусах.
Розв'язування:Якщо потрібно розкласти ф-ю по синусах, то вона повинна бути непарною.
А для того, щоб вона була непарною на (-2;2], запишемо її у вигляді
f(x)=x(2-|x|).
Таке довизначення не змінює її значень на заданому в умові інтервалі+дає можливість інтегрувати по синусах.
Перевіримо властивість коефіцієнтів ряду Фур'є:

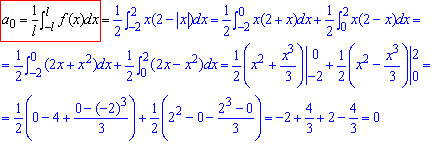
Отримали підтвердження, що для непарної f(x)=x(2-|x|) на (-2;2] значення коеф-ів a₀=0, a_k=0 рівні нулю.
Інтегруванням знаходимо b_k:

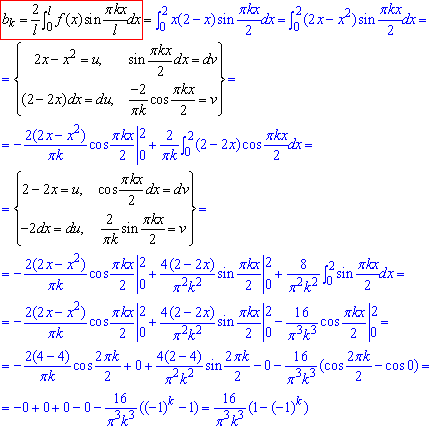
Кілька разів застосували інтегрування частинами, щоб спростити інтеграли.
Складаємо розклад функції в ряд Фур'є по синусах
.
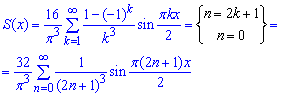Графік суми ряду S(x)

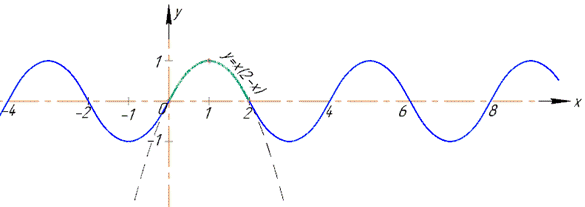
Перевіримо правильність обчислень побудовою перших 5 членів ряду в Мейпл
f := 16/(Pi^(3))*sum((1-(-1)^k)/k^3*sin(Pi*k*x/2), k= 1 .. 5);
plot(f, x = -2 .. 3, color = red);

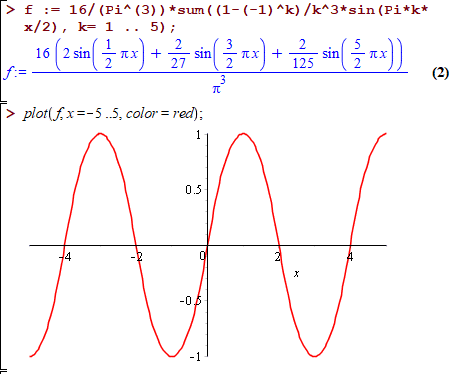
Приклад 17 Розкласти функцію f(x)=x-x²/2 в ряд на 0≤x≤1
а) по косинусах;
б) по синусах.
Розв'язування: А) Продовжимо функцію f(x)=x-x^2/2 на проміжок (-1;0) таким чином, щоб вона була парною на (-1;1], тоді f(x)=|x|-x^2/2.
Оскільки зараз f(x) парною на -1≤x≤1 , то b_k=0, а коефіцієнти Фур'є при косинусах обчислюємо інтегруванням:

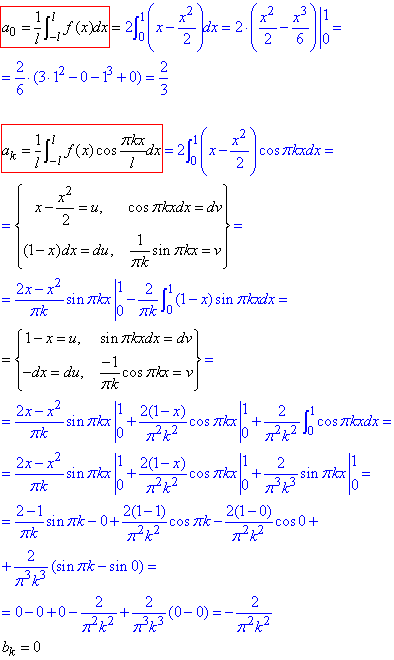
Записуємо розклад функції f(x)=|x|-x^2/2 в ряд Фур'є:

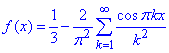
Побудуємо графік ряду в Мейплі для 5 перших членів розкладу:
f := 1/3-2*(sum(cos(2*Pi*k*x)/k^2, k = 1 .. 5))/Pi^2;
plot(f, x = -2 .. 1, color = red);

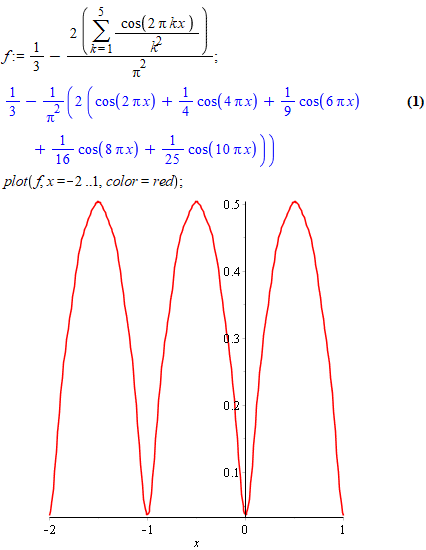
Функція парна і добре наближає досліджувану параболу f(x)=x-x^2/2.

Б) Для розвинення по ряду синусів, продовжимо функцію f(x)=x-x^2/2 на проміжок (-1;0] таким чином, щоб вона була непарною на (-1;1], тоді
f(x)=x(1-|x|/2).
Уважно перегляньте, та переконайтеся, що саме таке довизначення потрібно виконати.
Оскільки функція f(x) є парною на проміжку -1≤x≤1, то автоматично a₀=0 й a_k=0 і залишається проінтегрувати b_k:

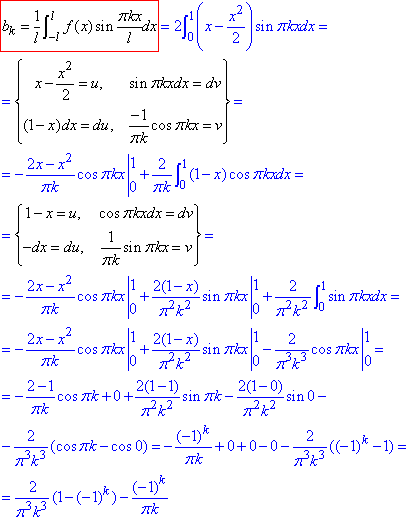
Отож, для заданої функції ряд Фур'є має вигляд:

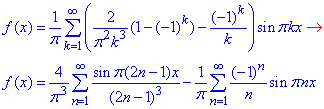
Графік перших 30 членів ряду має вигляд

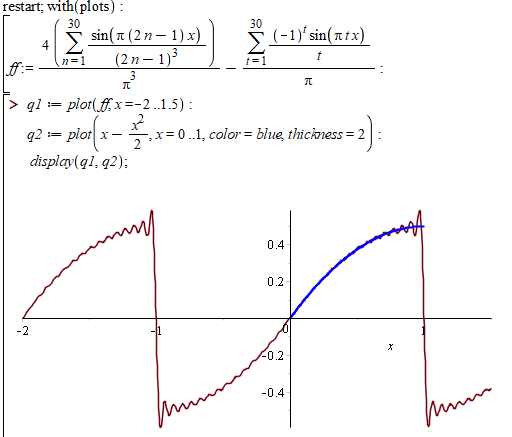
Далі навчимося розкладати в ряд Фур'є на [-Pi;Pi], вивчимо ряд теорем, познайомимося з комплексною формою Фур'є і обов'язково, все це закріпимо на практиці!