Розклад в ряд Фур'є інтегруванням. Рівність Парсеваля

Функція f(x) на проміжку (-π;π) можна розкласти в ряд Фур'є за формулою
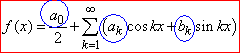(1)
де a₀, a_k, b_k - коефіцієнти Фур'є:
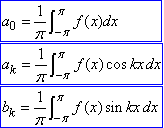(2)
Якщо функція f(x) парна на проміжку (-π;π), то всі коефіцієнти при синусах рівні нулю, а при косинусах рівні:
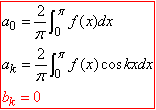(3)
Якщо функція f(x) непарна на проміжку (-π;π), то маємо розклад тільки по синусах, a_k=0
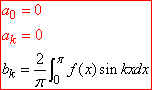(4)

Теорема (ознака) Діріхле: якщо функція f(x) періоду 2π кусково-монотонна на проміжку [-π;π] і має в ньому не більше, ніж скінченну кількість точок розриву (першого роду), то її ряд Фур'є збігається до суми f(x₀) у кожній точці неперервності й до суми

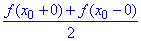
у кожній точці розриву.

Якщо функція f(x) інтегрована разом зі своїм квадратом на (-π;π) , то виконується:
рівність Парсеваля на проміжку (-π;π):


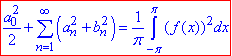
нерівність Бесcеля на проміжку (-π;π):

Нехай a_k, b_k - коефіцієнти Фур'є для функції f(x) і a'_k, b'_k - коефіцієнти Фур'є для функції f'(x) (похідної), тобто ряд на (-π;π) матиме вигляд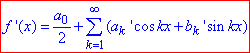
Тоді, знаючи коефіцієнти Фур'є для функції f'(x), можна отримати коефіцієнти Фур'є для функції f(x), які пов'язані залежностями:

У показниковій (комплексній) формі залежності матимуть вигляд

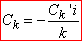
Схема розкладу в ряд Фур'є інтегруванням

Приклад 1. Проітнтегрувавши почленно розклад в ряд Фур'є функції

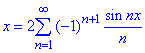
розвинути в ряд Фур'є на проміжку (-π;π) функції:
а) f(x)=x^2;
б) g(x)=x^3;
в) z(x)=x^4.
Розв'язування: Оскільки на проміжку (-π;π) ряд збігається рівномірно, а функція sin(nx) є неперервною, то проінтегруємо його почленно: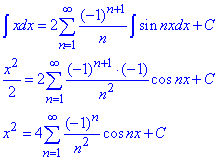
а) Для функції f(x)=x^2 константу C знайдемо, як коефіцієнт Фур'є С=a0/2 на проміжку (-π;π) :

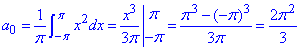
Остаточно для функції f(x)=x^2 на (-π;π) ряд Фур'є має вигляд:
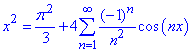(5)
б) Щоб отримати g(x)=x^3 виконаємо наступне: оскільки на проміжку (-π;π) отриманий ряд (5) збігається рівномірно, а функція cos(nx) є неперервною, то проінтегруємо ряд (5) почленно:

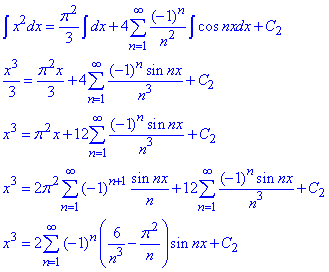
Оскільки функція g(x)=x^3 непарна, то за властивістю

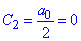
Таким чином, для функції g(x)=x^3 на (-π;π) ряд Фур'є має вигляд:
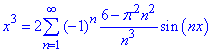(6)
в) Аналогічно знаходимо розвинення в ряд Фур'є для z(x)=x^4.
Отриманий ряд (6) збігається рівномірно на проміжку (-π;π) , крім того функція sin(nx) є неперервною, тому можемо проінтегрувати (6) почленно:

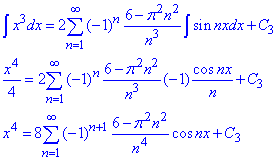
для z(x)=x^4 константу C3 довизначимо, як коефіцієнт Фур'є С3=a0/2:

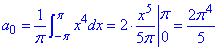
Підставляємо сталу в ряд та отримаємо кінцеву формулу ряду Фур'є для функції z(x)=x^4:

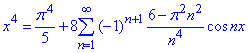
За отриманими рядами легко можна перевірити у справедливості формули:

які відповідають функціям f'(x) і f(x) на (-π;π) .

Подібні задачі Ви по аналогії зможете повторити, розглянемо складніші умови.

Приклад 2. Проінтегрувавши почленно розвинення

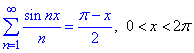
отримати формулу

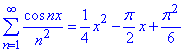
Розв'язування: Можна перевірити, що для функції f(x)=(π-x)/2 заданий ряд

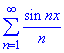
є рядом Фур'є, який за теоремою Діріхле збігається до f(x) на проміжку 0<x<2π.
Проінтегруємо почленно задану рівність:

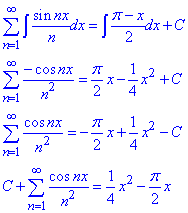
Сталу інтегрування C знайдемо з умови, що для функції 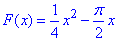отриманий ряд

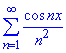
є рядом Фур'є, який за теоремою Діріхле збігається до F(x) на проміжку 0<x<2π.
Тоді стала C є не що інше, як коефцієнт a0/2 в формулі Фур'є, тому його і знаходимо

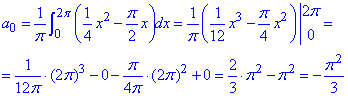
Підставляємо в розвинення ряду, і виражаємо суму

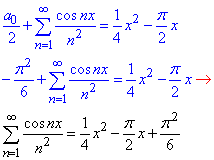
Отримали потрібну суму ряду, що і треба було довести.

Приклад 3. Розвинути в ряд Фур'є функцію:
f(x)=cos(αx) в інтервалі [-π;π], де α∉Z.
За допомогою отриманого розвинення довести, що

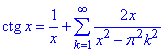
Розв'язування: Схема розвинення в ряд наступна:
спершу інтегруванням обчислюємо коефіцієнти Фур'є. Так як косинус парна функція, то застосовуємо формулу (3):
(вона виділена в інтегралах, щоб Ви не гортали сторінкою, а вчилися інтегрувати)

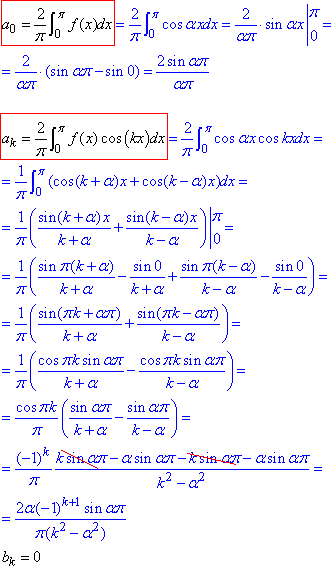
Далі, маючи коефіцєнти,складаємо ряд Фур'є за формулою (1)

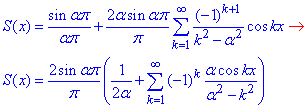
Перша частина завдання виконана.
2) Для доведення формули котангенса використаємо наступні міркування.
Оскільки функція f(x)=cos(αx) в інтервалі [-π;π] неперервна і кусково-монотонна, то за теоремою Діріхле S(x)=f(x)=cos(ax) на [-π;π] , тоді, прирівнюючи і переносячи синус при x=π, отримаємо:

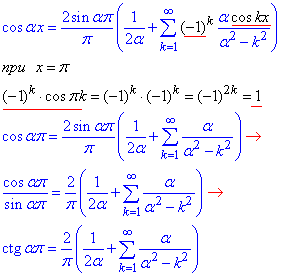
Далі в знайдене розвинення котангенса вводимо заміну α=x/π (за умовою α не є цілим числом) та розписуємо

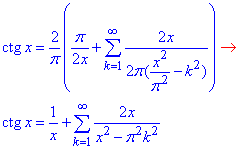
Остання формула і є шуканою, яку потрібно було вивести.

Теорема Персеваля

Приклад 4.За допомогою рівності Парсеваля для функції

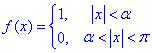
знайти суми рядів

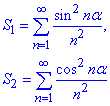
Розв'язування: Функція f(x) парна на проміжку (-π;π), тому матиме розвинення лише за косинусами.
Обчислюємо коефіцієнти перетворення Фур'є

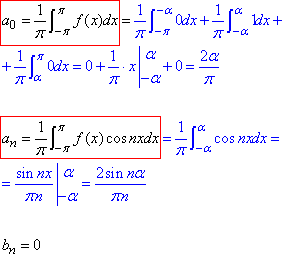
Далі застосовуємо рівність Парсеваля
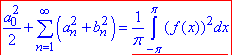(7)
де права сторона рівна:

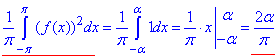
Підставляємо в формулу (7)(рівність Парсаваля) коефіцієнти та інтеграл по функції:

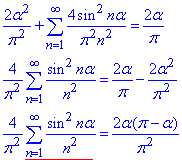
звідси виражаємо потрібну суму S1

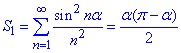
2) Використовуючи основну тригонометричну тотожність sin²(x)+cos²(x)=1, виведемо формулу для суми S2:

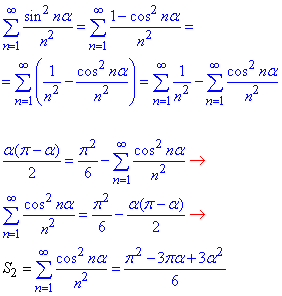
ІІ спосіб (для аналізу)
Для заданої функції f(x) розвинемо ряд Фур'є по синусах.
Тоді продовжимо функцію f(x) на проміжок (-π;0) так, щоб вона була непарною на (-π;π).
Тоді коефіцієнти ряду Фур'є для непарних функцій рівні

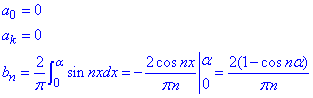
Отримані коефіцієнти Фур'є знову підставимо у рівність Парсеваля:

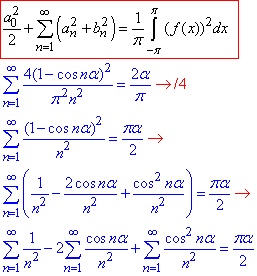
Використовуючи раніше зроблені вправи, маємо

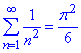
(практичне заняття 4, вправа 3),

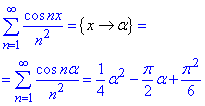
(практичне заняття 6, вправа 2).

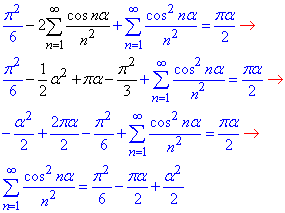
звідси отримуємо потрібну суму S2

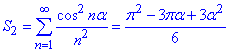
Попереду ще багато розв'язків на ряди Фур'є. Умови до завдань взяті з практичних, тому будуть корисними в першу чергу студентам, а далі викладачам і всім хто розв'язує задачі, які без формул Фур'є не вирішити.