Побудова графіків ліній рівня

На попередньому ввідному уроці було дане означення лінії рівня, поверхні рівня, та області визначення для функції багатьох змінних (ФБЗ).
Продублюємо, що таке лінії рівня та перейдемо до практичних де навчимося будувати графіки лінії рівня, зокрема в математичному пакеті Мейпл.
Означення: Якщо функція u є функцією двох змінних x і y, тобто u=f(x;y), то лінії на площині, що задаються рівнянням
f(x;y)=c – називаються лініями рівня.

Побудова графіків ліній рівня

Приклад 1. Побудувати лінії рівня наступних функцій z=x+y,
Розв'язування: Складаємо рівняння ліній рівня та міркуємо, що вони описують
x+y=c,
y=-x+c.
Отримали множину паралельних прямих.

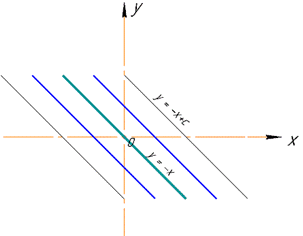
Тут і надалі c - довільна константа.

Приклад 2. Побудувати лінії рівня функції двох змінних
u(x, y)=x²-y².
Розв'язування: Щоб скласти рівняння ліній рівня прирівнюємо праву сторону до сталої
x²-y²=c.
Дістанемо множину рівносторонніх гіпербол зі спільними асимптотами y=±x, де c≠0.
Схематичний рисунок ліній рівня наведено нижче

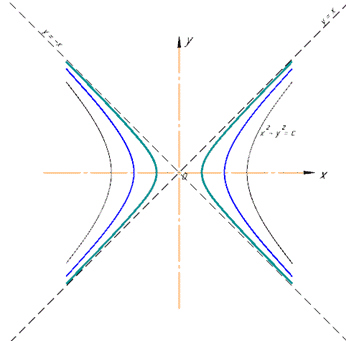
При с=0 асимптоти y=±x стають лініями рівня.

Приклад 3. Зобразити лінії рівня функції
F(x, y)=1/(x²+2y²)
Розв'язування: Прирівняємо праву сторону до сталої та зведемо отримане рівняння до канонічного вигляду

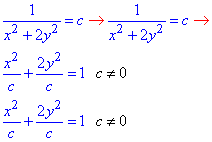
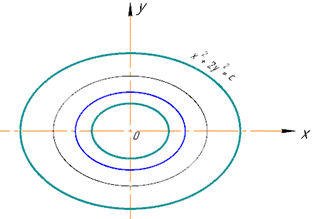
Лініями рівня функції F буде множину подібних еліпсів.

Приклад 4.Схематично зобразити лінії рівня
z=min(x, y).
Розв'язування: Складаємо рівняння та, в залежності від значень аргументу, знаходимо розв'язки
min(x, y)=c,

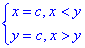
Отримали множину сторін кутів, які паралельні додатнім напрямкам координатних осей Ox і Oy з вершинами на прямій y=x.
Рисунок ліній рівня наступний

Лінії рівня в Мейпл

Приклад 5. Встановити та зобразити лінії рівня функції
z(x, y)=x²+y².
Розв'язування: Виписуємо рівняння, яке під силу визначити усім школярам
x²+y²=c.
Отримали множину концентричних кіл з центром в початку координат.
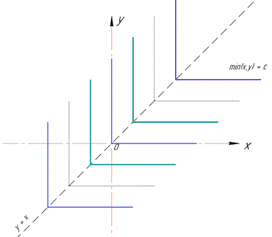
Покажемо як будувати кола в Мейпл

Приклад 6. Визначити лінії рівня функції
z=x^y, (x>0).
Розв'язування:  Розписуємо рівняння 
x^y=c,
Логарифмуємо обидві частини
ln(x^y)=ln(c),
y•ln(x)=c.
Лініями рівня z(x,y)=x^y, (x>0) є множина кривих y=c/ln(x).
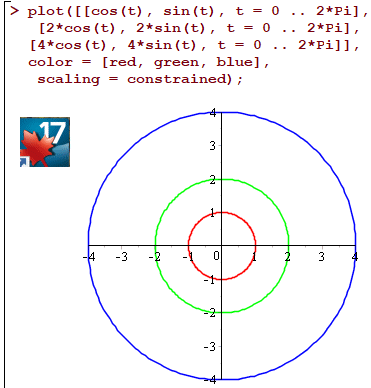
Побудуємо графіки в Мейпл для додатних та від'ємних сталих:

Приклад 7. Знайти та побудувати лінії рівня
z=x^ye^-x.
Розв'язування: Записуємо рівняння лінії рівня та виражаємо з нього y(x,c):

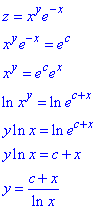
Лініями рівня є множина кривих y=(c+x)/ln(x).
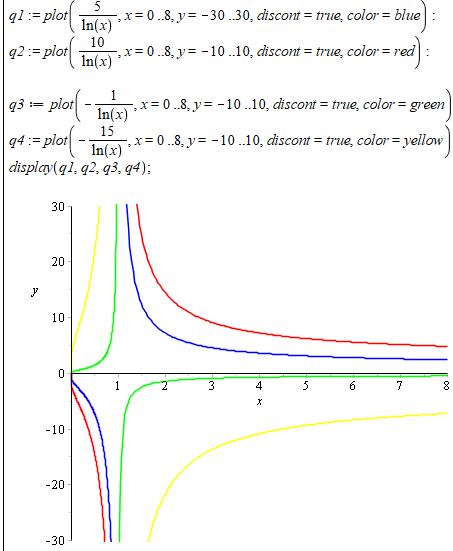
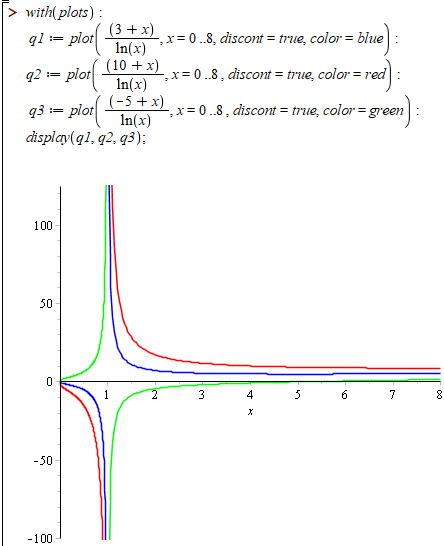
Наведемо код для побудови ліній рівня в Maple
with(plots);
q1 := plot((3+x)/ln(x), x = 0 .. 8, discont = true, color = blue);
q2 := plot((10+x)/ln(x), x = 0 .. 8, discont = true, color = red);
q3 := plot((-5+x)/ln(x), x = 0 .. 8, discont = true, color = green);
display(q1, q2, q3);
Тут команда with(plots); підключає бібліотеку для роботи з графікою
display - виводить кілька графіків одночасно.
discount - функція, яка дозволяє будувати графік неперервно, або з асимптотами (розривно).

Приклад 8. Побудувати лінії рівня функції двох змінних
z(x, y)=√x√y.
Розв'язування: Прирівнюємо функцію до сталої та виражаємо y(x)

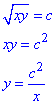
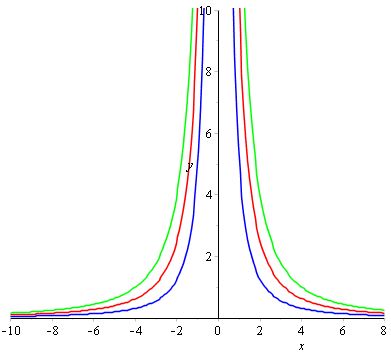
Лініями рівня є множина рівносторонніх гіпербол, які знаходяться в І і ІІ квадрантах, асимптотами є осі координат Ox і Oy.
Наведемо код в Мейплі для побудови графіка
q1 := plot(5/x^2, x = -10 .. 8, y = 0 .. 10, discont = true, color = blue);
інші 2 криві для с²=10 та с²=16.

Далі навчимо Вас будувати поверхні рівня та обчислювати границі та екстремуми функцій багатьох змінних.