Розклад функції в ряд Фур'є на проміжку [-l;l]

Функція f(x) на проміжку [-l;l] розкладається в ряд Фур'є за формулою
(1)
де a₀,a_k,b_k - коефіцієнти Фур'є, які знаходять інтегруванням:
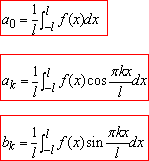(2)

Алгоритм розкладу функцій в ряди Фур'є

Розглянемо поширені на практиці завдання на розвинення в ряд Фур'є. Розпочнемо зі сталих і лінійних функцій, а завершимо квадратичною функцією та експонентою.

Приклад 1. Розвинути в ряд Фур'є функцію:

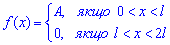
Розв'язування: Бачимо, що задана функція є кусково сталою.
Тому при обчисленні коефіцієнтів Фур'є за формулами (2) інтеграл ділиться на 2:

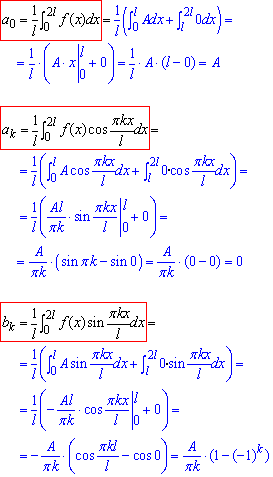
Як бачите, інтеграли не складні.
Якщо задана функція складається з більшої кількості кусково неперервних функцій, то інтегруємо кожну з них на інтервалі де вона задана. При цьому множник перед інтегралом 1/l рівний половині проміжку на якому задана функція.
Складаємо ряд Фур'є для заданої функції за формулою (1):

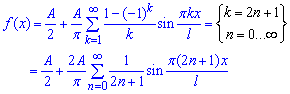
Звикайте, що основні формули для обчислень будуть виділені з прикладу в приклад. Це зроблено з метою, щоб Ви візуально запам'ятовували формули Фур'є для коефіцієнтів розкладу функції в ряд.

Приклад 2. Знайти розклад  в ряд Фур'є функції  f(x)=x на (a;a+2l).
Розв'язування: Обчислюємо коефіцієнти Фур'є інтегруванням:

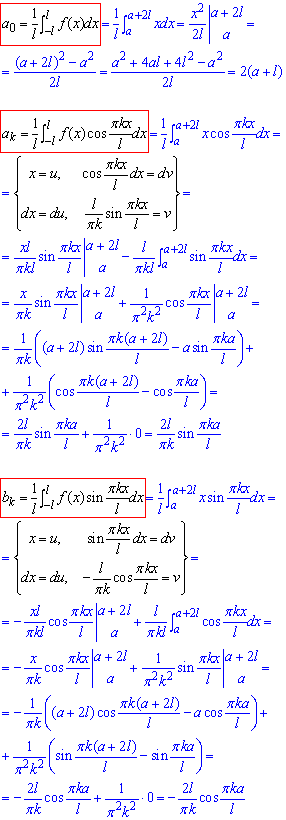
Записуємо для лінійної функції ряд Фур'є:

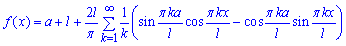
Якщо Ви один раз знайшли невизначені інтеграли для лінійних, квадратичних чи інших функцій, то результати можете повторно використовувати для знаходження інтегралів від комбінацій цих функцій. Адже на практиці у Вас міняються лише межі інтегрування, підінтегральні функції часто будуть або пропорційними, або містити комбінації вже розглянутих раніше функцій.

Приклад 3. Знайти розклад в ряд Фур'є функції:
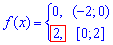на (-2;2].
Розв'язування: За схемою обчислюємо коефіцієнти Фур'є, якщо розмах (l=2):

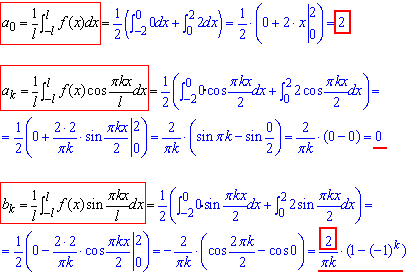
Якщо половина проміжку інтегрування не змінюється l=2, то коефіцієнти в розкладі Фур'є змінюються пропорційно (k=2) до початкової функції f(x)={2}.
Записуємо знайдений розклад функції в ряд Фур'є:

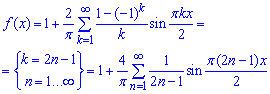
На цьому приклад розв'язано.

Приклад 4. Розвинути в ряд Фур'є функцію:
f(x)=4-x на (2;6], T=4.
Розв'язування: Визначимо коефіцієнти Фур'є (l=2):

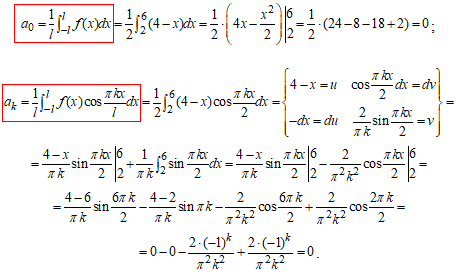
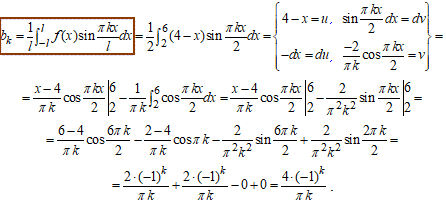
Далі за формулою Фур'є (1) складаємо розвинення функції f в ряд:

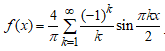
Приклад 5. Розвинути в ряд Фур'є функцію f(x)=e^x на (-2;2].
Розв'язування: Визначимо коефіцієнти Фур'є при l=2:

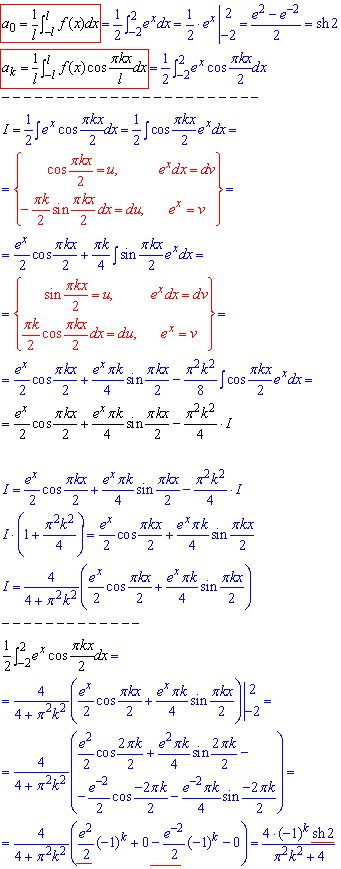
При знаходженні a_k застосували правило інтегрування частинами.
*) Зауваження: для спрощення використали формулу гіперболічного синуса:

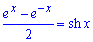
Далі обчислюємо коефіцієнти при розвиненні за синусами b_k:

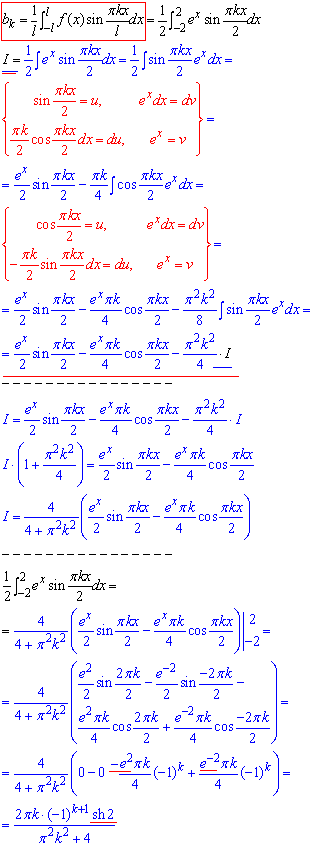
Пригадуємо формулу розкладу функції в ряд Фур'є

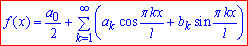
та підставляємо знайдені коефіцієнти a₀, a_k, b_k:

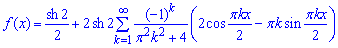
На практичних у Вас будуть дещо інші функції, однак якщо вони належать до класу тих, які розглядали, то інтеграли від них Ви можете швидко виписати, враховуючи вище розписані інтеграли.
На наступному уроці продовжимо аналізувати готові приклади на ряди Фур'є.