Доведення ортогональності функцій з вагою ρ(x)

На попередньому уроці ми частково розглянули доведення ортогональності функцій, вивчили наступну теорему.

Теорема 1: Нескінченна система функцій φ₁(x), φ₂(x),..,φ_n(x),.. називається ортогональною на відрізку [a;b], якщо при будь-яких n≠k виконується рівність 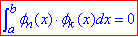(1)
при цьому норма функцій не дорівнює нулю
(2)

Сьогодні на практичних навчимося доводити ортогональність функцій з вагою ρ(x):

Теорема 2: Система функцій 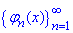ортогональна на відрізку [a;b] з вагою ρ(x)≥0, якщо інтеграл рівний нулю
(3).
Додатково повинна виконуватися умова (2), де до добутку додається множник ρ(x).
Щоб закріпити на практиці доведення ортогональності функцій розглянемо кілька готових прикладів з математичного аналізу.

Приклади на доведення ортогональності функцій з вагою ρ(x)≥0

Почнемо з завдання на 1 теорему, наступні на доведення умов теореми 2.

Приклад 5. Довести, що система функцій {cos(n·x), n=1..∞} ортогональна на [0;π];
Доведення:Через інтеграл перевіряємо чи виконується умова (1) ортогональності функцій

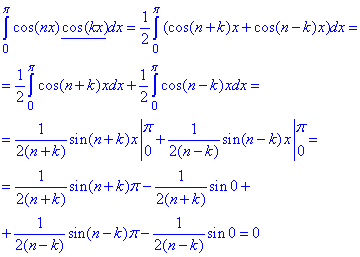
Інтеграл рівний нулю, отже 1 умова теореми 1 виконується.
Обчислюємо інтеграл - "умова нормування"

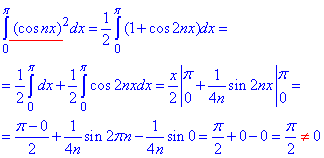
Він відмінний від нуля, відповідно довели, що система функцій {cos(nx), n=1..∞} ортогональна на [0;π].

Приклад 6. Довести, що система функцій 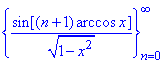ортогональна з вагою ρ(x)=√(1-x^2) на проміжку [-1;1]:

Доведення: Перевіряємо чи виконується умова теореми 2:

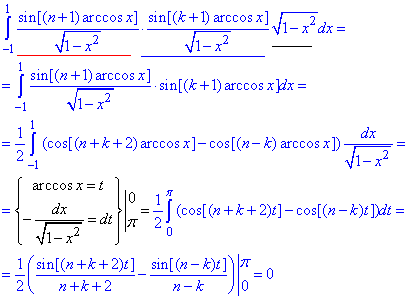
Тут використали заміну змінних під інтегралом, що автоматично привело до зміни меж інтегрування. ( Не забувайте про цей момент в обчисленнях.)
Інтеграл рівний нулю, отже задані функції ортогональні.
Перевіримо умову нормування

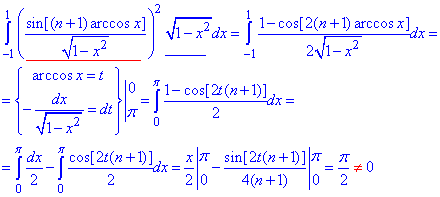
Норма функцій не рівна нулю (=π/2), таким чином довели, що система функцій ортогональна на проміжку [-1;1] з вагою ρ(x).

Приклад 7. Довести, що система функцій {1/x·sin(Pi·nx/l)} ортогональна з вагою ρ(x)=x², ρ(x)≥0 на проміжку [0;l].

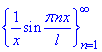
Доведення: Вага в даному прикладі допомагає спростити інтеграл, тому без проблем доводимо, що перша умова теореми про ортогональність функцій виконується

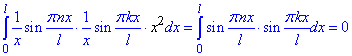
Далі залишається перевірити умову, що норма функцій не рівна нулеві

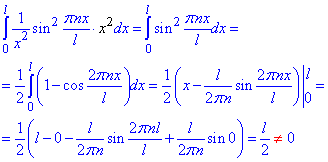
Обидві умови ортогональності функцій виконуються, тому твердження про ортогональність ф-й {1/x·sin(Pi·nx/l)} з вагою ρ(x)=x^2 вірне.
Далі йдуть уроки, які вчать знаходити норму функцій та розкладати їх в ряди Фур'є за синусами та косинусами.
Думаю, що після прочитаного Ви зможете довести ортогональність функцій самостійно!