Коефіцієнти Фур'є для парних і непарних функцій. Приклади розкладу в ряд

Функція f(x) на проміжку [-l;l] має розклад в ряд Фур'є
(1)
де a₀,a_k,b_k - коефіцієнти Фур'є, які обчислюють за формулами:
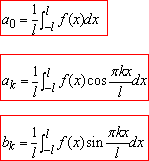(2)

Властивості коефіцієнтів Фур'є

1. Якщо функція f(x), яку розкладаємо в ряд непарна відносно початку координат то коефіцієнти a_k=0 рівні нулю, а b_k знаходять за формулою.

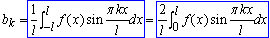
2. Якщо функція f(x) парна на [-l;l] то b_k=0, тоді як a_k обчислюють за формулою:

Тобто якщо функція парна відносно точки (0;0), то отримаємо розклад тільки за косинусами, якщо непарна - синус розвинення ряду Фур'є.

Продовжуємо попередній урок і сьогодні розберемо завдання із "Збірник задач.." за редакцією В. П. Дубовика, І. І. Юрика.

Приклад 396. Знайти розклад в ряд Фур'є функції f(x)=x на (-1;1].
Розв'язування: Повторюємо алгоритм з попереднього уроку:
визначимо коефіцієнти розкладу для l=1 інтегруванням.

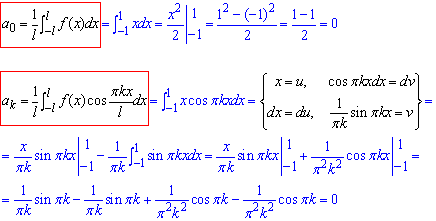
Інтегруванням ми довели, що для непарної функції f(x) на [-l;l] коефіцієнти a₀=0, a_k=0 рівні нулю.

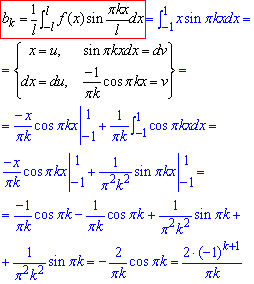
З формули слідує, що для непарної функції f(x) на [-l;l] маємо

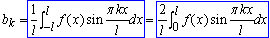
Це відповідає властивості (2)
Записуємо ряд Фур'є для f(x):

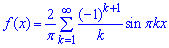
Приклад 398. Розвинути функцію f(x)=4-x^2 в ряд Фур'є на проміжку (-2;2].
Розв'язування: Визначимо коефіцієнти Фур'є (l=2), враховуючи, що функція f(x)=4-x^2 парна на (-2;2]:

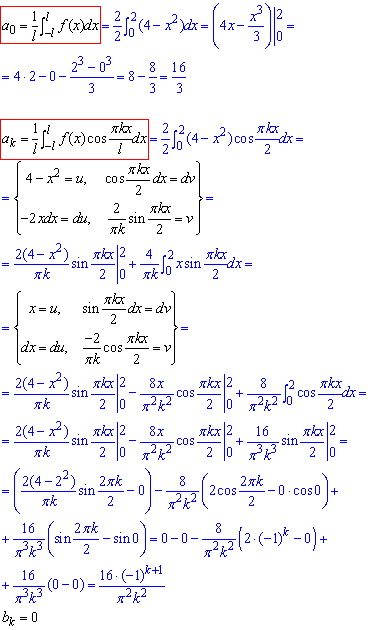
Записуємо розклад в ряд Фур'є за косинусами:

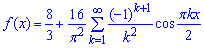
Порівняйте кінцеву формулу розкладу з попереднім прикладом. При розвиненні непарних функцій маємо лише ряд за синусами, при розкладі парних функцій відсутні члени ряду за синусами, тобто маємо сталу + розвинення за косинусами.

Приклад 397. Знайти розвинення в ряд Фур'є функції

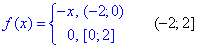
Розв'язування:Уважно перегляньте умову, тут функція насправді ні парна ні непарна. Хоча "-х" є непарною відносно початку координат, проте в умові вона не задається на всій множині розвинення в ряд. Тому в таких випадках слід визначати усі коефіцієнти Фур'є:

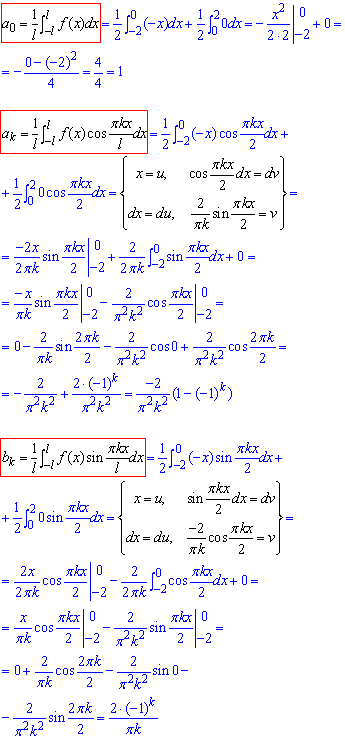
Повторіть правило інтегрування частинами, ми часто будемо його застосовувати.
Будуємо ряд Фур'є для заданої функції:

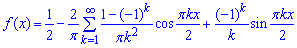
Приклад 399. Розкласти в ряд Фур'є функцію

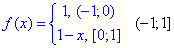
Розв'язування: Починаємо аналізувати, що нам задано. Функція кусково неперервна, водночас ні парна ні непарна.
Тому інтегруванням обчислюємо усі коефіцієнти Фур'є (l=1):

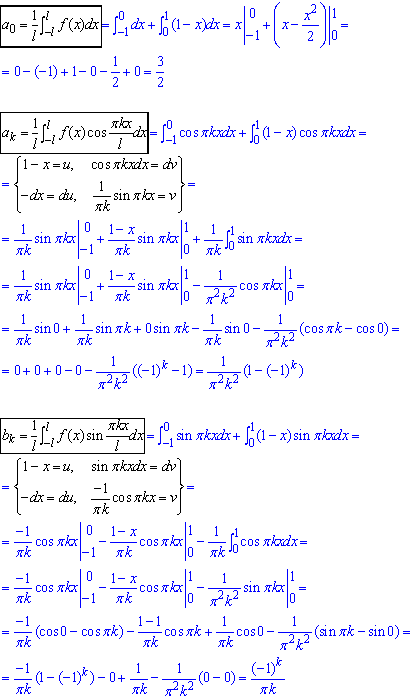
Розклад функції в ряд Фур'є:

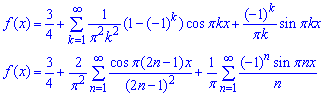
Не думайте, що на практичних чи підсумкових роботах будуть легші завдання. Практикуйте побільше самостійно і беріть наведені приклади за підказки при обчисленні інтегралів, поступово побачите, що багато повторюється.
Далі розберемо відповіді на ряди Фур'є задані на (-π;π], розклад періодичних функцій та багато чого, що Вас вчитимуть в курсі математичного аналізу.