Сьогодні розберемо приклади на розклад в ряд Фур'є функцій, які є періодичними на проміжку[-Pi;Pi]. Це можуть бути функції як вигляду sin(kx), cos(mx), так і їх комбінація.
Пригадаєм тригонометричну форму ряду Фур'є
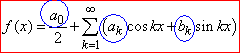(1)
a0, ak, bk - коефіцієнти Фур'є знаходять інтегруванням:
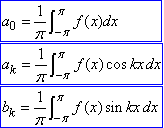(2)
Перейдемо до практичних.
Приклад 24 Розвинути в ряд Фур'є функцію f(x)=cos(2x) на (0;π] по синусах.
Розв'язування: На попередніх уроках була розібрана методика довизначення функцій на весь і нтервал, та показано, що робити коли потрібно знайти розвинення в ряд тільки по синусах чи по косинусах.
Розкласти по синусах означає продовжити функцію f(x)=cos(2x) так, щоб вона була непарною на (-π;0]. Оскільки косинус за визначенням парна, то нічого не залишається, як подати її у вигляді
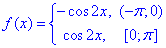
Тоді її можемо розкласти в ряд Фур'є по синусах.
Обчислимо коефіцієнти Фур'є:
з непарності f(x) слідує, що a0=0 і ak=0, і залишається проінтегрувати bk:
Записуємо розклад в ряд Фур'є по синусах за формулою (1):
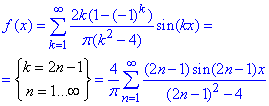
Тут замною індексів k=2n-1 позбуваємося частини ряду для яких множник 1-(-1)^k =0 для парних k=2n.
Як побудувади графік суми ряду Фур'є?
Щоб отримати графік ряду Фур'є S(x) потрібно графік функції 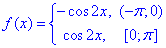симетрично копіювати з інтервалу де вона визначена [-Pi;Pi] на наступні (π;2π] і т.д, та попередні (-2π;-π]. Далі з'єднати точки в місцях розриву функції x=πk, k∈Z.
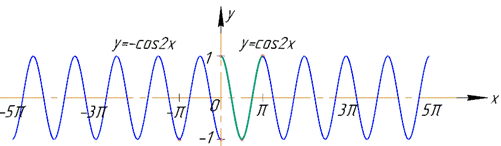
Якщо отримаєте подібний графік, то Ви поспішили, оскільки не дослухались порад, та не скопіювали графік з інтервалу [-Pi;Pi] на сусідні.
Для порівняння, побудуємо графік перших 50 членів ряду S(x) в Мейплі
g := 4/Pi*sum((2*n-1)/((2*n-1)^2-4)*sin((2*n-1)*x), n=1..50):
plot(g, x = -Pi .. 3*Pi, color = red);
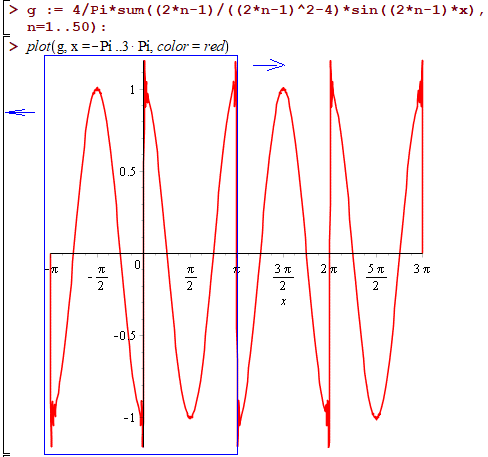
Порівняйте з отриманим вище графіком і проаналізуйте, які з помилок допущені.
На попередніх уроках наведено чимало графіків рядів Фур'є, то ж можете переглянути та проаналізувати їх побудову.
Приклад 25. Знайти розклад в ряд Фур'є функції f(x)=|sin(3x)| на проміжку (-π;π].
Користуючись здобутим результатом, знайти суму ряду
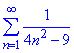
Розв'язування: Починаємо аналізувати на парність непарність.
Функція f(x)=|sin(3x)| парна на проміжку (-π;π), тому отримаємо ряд ряд Фур'є за косинами, а коефіцієнти bk=0.
Використовуємо формули коефіцієнтів розкладу ak для парних функцій:
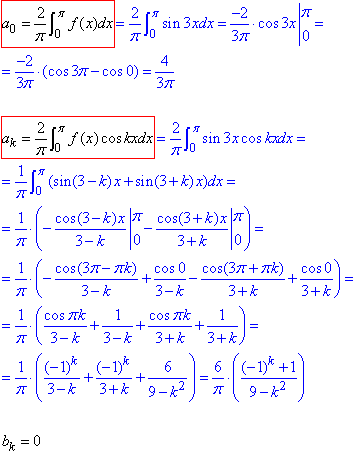
Складаємо ряд Фур'є по косинусах:
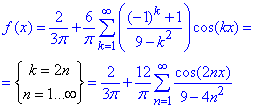
При зміні індексів враховано, що для непарних k=2n+1 множник (-1)^k+1 =0 рівний нулю.
Будуємо графік суми ряду S(x)
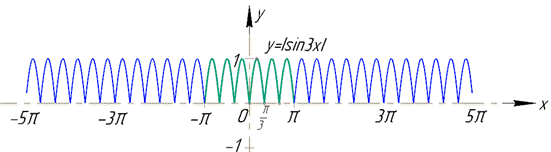
2) Щоб знайти суму числового ряду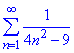 
коли маємо розклад f(x)=|sin(3x)| в ряд:
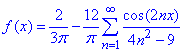(3)
необхідно, щоб в розкладі косинуси були рівні одиниці
cos(2nx)=1.
Це досягається в точці x=0.
Сума знайденого ряду Фур'є збігається до f(x)=|sin(3x)|, тому при x=0 дістанемо f(0)=0.
Далі x=0 підставляємо в (3) та спрощуємо
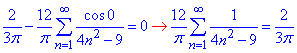
звідси виражаємо потрібну суму числового ряду
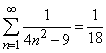
Подібним чином обчислюються всі приклади, де потрібно знайти підряди які випливають з розкладу f(x).
Далі йдуть завдання зі Збірника задач Б. П. Демидовича.
Приклад 26 (2946). Розвинути в ряд Фур'є:
f(x)=sin(ax) в інтервалі (–π;π] (a - не ціле).
Розв'язування: Обчислимо коефіцієнти Фур'є. Так як функція f(x)=sin(ax) непарна на (–π;π], то a0=0 і ak=0;
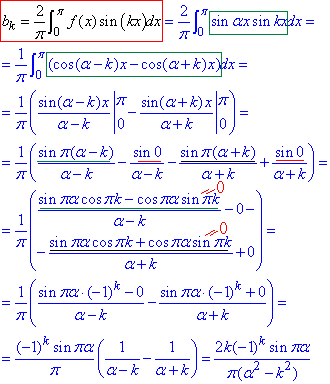
Складаємо для f(x)=sin(ax) ряд Фур'є:
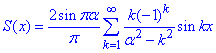
Уважно розберіть інтегрування, без знання відповідних формул Ви не зможе проінтегрувати добуток синусів чи косинусів.
Приклад 27 (2951).Розкласти в ряд f(x)=x•cos(x) в інтервалі (–π/2;π/2).
Розв'язування: Оскільки функція f(x)=x•cos(x) непарна на заданому інтервалі, то a0=0 і ak=0.
Коефіцієнти при синусах дістанемо інтегруванням, попередньо розписавши добутки синусів
Перегляньте, як вдалося спростити формули завдяки переходу від синусів до косинусів і навпаки. Застосовуйте наведені результати в подібних прикладах.
Виписуємо ряд Фур'є для досліджуваної ф-ї: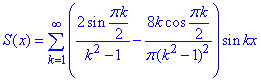 
Щоб більше зрозуміти тему переглядайте попередні уроки, оскільки матеріал добре засвоюється коли Ви читаєте уроки від першого до останнього. Тоді в комплексі Ви бачите, на яких моментах уже раніше зупинялися і при вивченні нових формул, теорем базове Ви вже повинні розуміти.
Далі розберемо комплексну форму ряду Фур'є та навчимо Вас розв'язувати відповідні завдання.
