Комплексна форма ряду Фур’є на (-π;π). Приклади

Комплексна форма ряду Фур'є на проміжку (-π;π) має вигляд
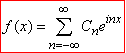(1)
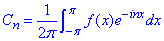- комплексні коефіцієнти Фур'є. n=0,±1;±2,...
Комплексна форма ряду Фур'є на проміжку (-l;l) має вигляд
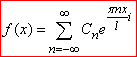(2)
де 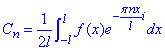- комплексні коефіцієнти Фур'є. n=0,±1;±2

Формула Ейлера:

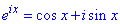
звідси випливає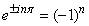
Тригонометричні функції у комплексній формі:

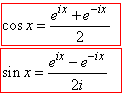
Приклади розкладу функції в комплексний ряд Фур'є

Приклад 1. Використовуючи наступні формули

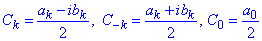
довести еквівалентність між показниковою та тригонометричною формами ряду Фур'є.
Доведення: Маємо суму ряду 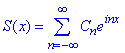у показниковій формі, тоді

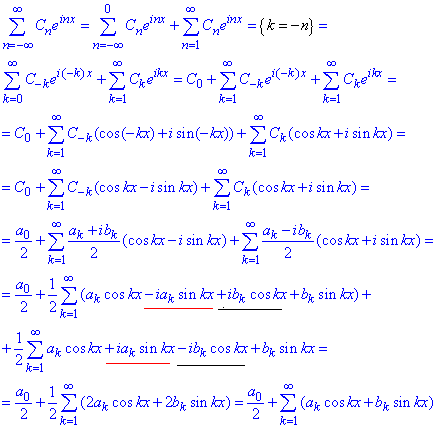
Отримали суму ряду

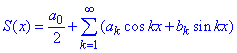
у тригонометричній формі, що і треба було довести.

Приклад 2. Розвинути в комплексний ряд Фур'є функцію f(x)=e^x в інтервалі [-π;π].
Розв'язування:Обчислимо коефіцієнти Фур'є.

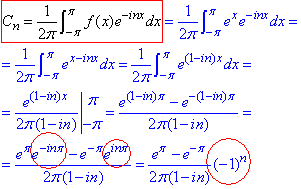
Перегляньте наведений інтеграл, оскільки при комплексному представленні тільки такі і будете отримувати.
За формулою (1) складаємо розклад функції в ряд Фур'є:

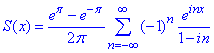
Коефіцієнт

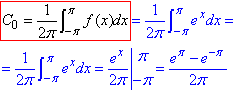
враховано в сумі S(x) при n=0.

Приклад 3. Розвинути в комплексний ряд Фур'є функцію:

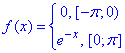
на [-π;π].
Розв'язування: Обчислюємо коефіцієнти розкладу C_k.

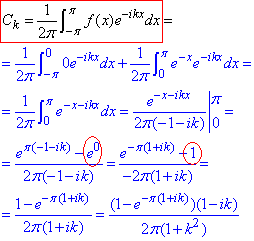
Наприкінці домножили і поділили на спряжений вираз до знаменника, щоб позбутися комплесної "i".
Ви повинні добре володіти інтегруванням, щоб використовувати як інструмент при вивченні даної теми. Якщо не знаєте інтегрування, то подібного значення Вам не отримати. Формули не складні якщо проаналізувати і все нове ми поступово Вам даємо та розписуємо до деталей.
Формули теж надіємось читабельні та відображають суть переходів між інтегралами.

Отож, для заданої функції ряд Фур'є має вигляд:


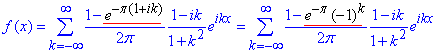
Нульовий коефіцієнт

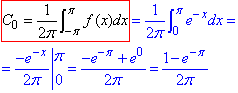
входить в суму ряду S(x) при k=0.

Приклад 4. Розвинути в комплексний ряд Фур'є функцію f(x)=x² в інтервалі [-π;π].
Розв'язування: Для обчислення коефіцієнтів Фур'є під інтегралом вводимо заміну змінних. Запам'ятайте її, адже потім не зможете взяти інтеграл, коли буде задана лінійна, квдратична чи старших порядків функція

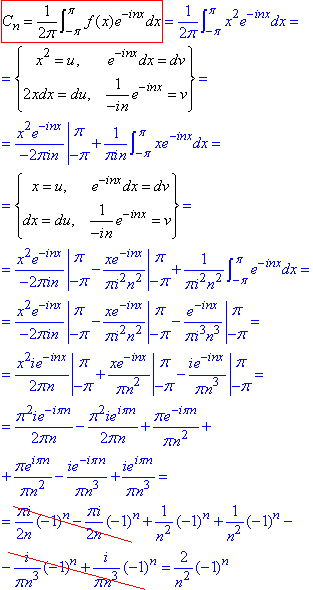
Зроблені тут заміни та самі значення неозначених інтегралів Ви можете використати якщо Вам задана функція виду f(x)=a*x².
Бачимо, що в нулі в знаменнику маємо особливість, тому додатково обчислюємо коефіцієнт при n=0:

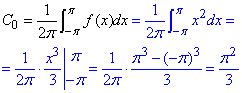
Складаємо розвинення в ряд Фур'є ф-ї f(x)=x²:

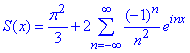
На цьому ще один приклад розв'язано.

Приклад 5. Розвинути в комплексний ряд Фур'є модуль функцію:
F(x)=|x| в інтервалі [-π;π].
Розв'язування: При визначенні коефіцієнтів Фур'є розділяємо інтегрування на дві області, а далі інтегруємо частинами

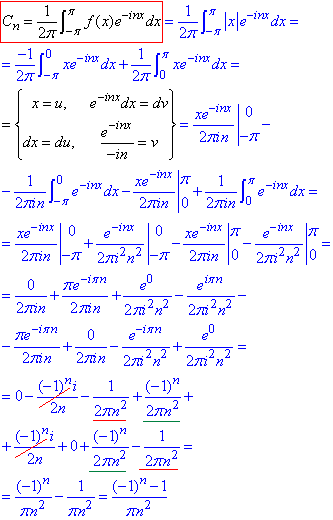
В знаменнику бачимо "n", тому додатково знаходимо C₀:

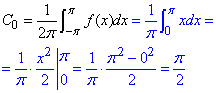
Комплексний ряд Фур'є має досить просту формулу в порівнянні з тригонометричним записом, тому обчисливши кілька прикладів самостійно Ви без проблем запишете суму ряду:

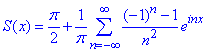
Приклад 6. Знайти комплексну форму ряд Фур'є для функції f(x)=exp(ax), a≠0 в інтервалі (–π;π).
Розв'язування: Розвинемо ряд Фур'є у комплексній формі.
Обчислюємо коефіцієнти:

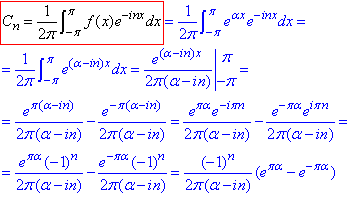
Підставляємо в комплексну форму ряду:

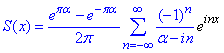
Враховуючи формулу Ейлера

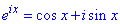
а також властивості суми

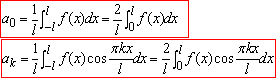
отримаємо

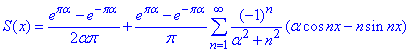
заданий ряд Фур'є у тригонометричній формі

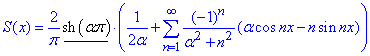
де 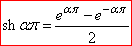- гіперболічний синус.

Приклад 7. Записати комплексну форму інтегралу Фур'є для функції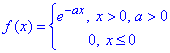

Розв'язування:Обчислюємо інтеграл за наведеною далі формулою:

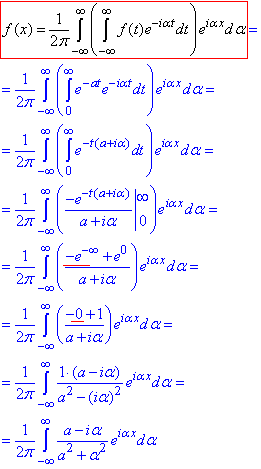
Інтегрування експонент не важке, під інтегралом виконали граничні переходи, які Ви повинні навчитися виконувати при обчисленні подібних задач.

Як бачите нічого складного окрім інтегрування в подібних прикладах Вас не чекає, тому підтягуйте інтегрування до належного рівня та вправляйтесь побільше з подібними завданнями самостійно.