Повний диференціал функції двох, трьох змінних

На уроці навчимося обчислювати диференціали функцій двох та трьох змінних. Спершу наведемо формули та правила обчислення диференціалів, а далі готові приклади знаходження диференціалів I та II порядку.

Нехай задана функція u=f(x;y;z), яка диференційовна в кожній точці області визначення. Тоді для неї існує повний диференціал:

Диференціал І порядку

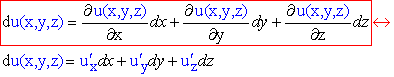
Диференціал II порядку та старших

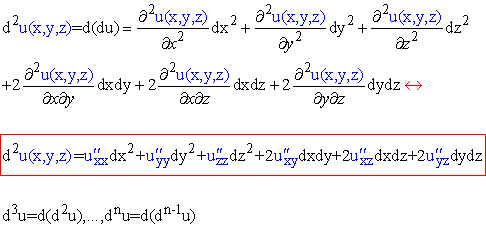
Поклавши одну зі змінних рівною нулю отримуємо формули повних диференціалів для функції двох змінних

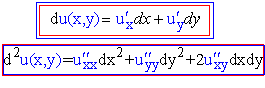
Правила диференціювання суми, добутку, та частки функцій

Якщо функції u(x,y,z), v(x,y,z) - диференційовні на області визначення, то справедливі формули

Якщо маємо складені функції наступного виду, то їх відповідні диференціали можна знайти за формулами:

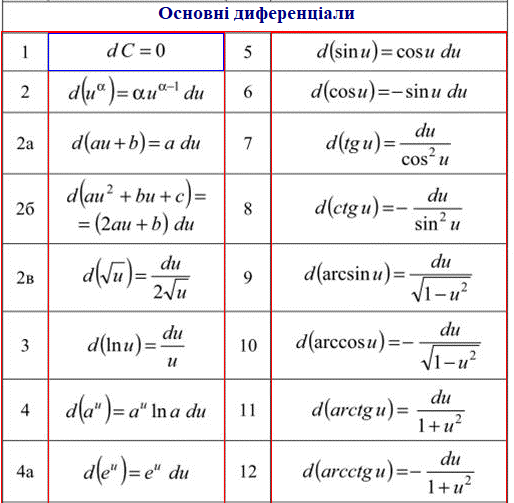
Наприклад, для функції u=e^x+y за формулою 4а диференціал першого роду рівний
du=d(e^x+y)=e^x+y·d(x+y)=e^x+y·(dx+dy),
диференціал 2 роду обчислюємо за правилом
d²u=d(du)=d(e^x+y·(dx+dy))=e^x+y·dx²+2e^x+ydxdy+e^x+ydy².
Для функцій багатьох змінних має місце інваріантність форми (першого) диференціала, як і для функції однієї змінної!

Далі розберемо готові розв'язки з практичних, які Ви повинні знати як робити та оформляти. Основні формули потрібні для обчислень будуть підкреслені червоним прямокутником.

Знайти диференціали першого і другого порядку f(x, y)

Приклад 1.1 u=x^m∙yⁿ, (x, y - незалежні змінні)
Обчислення: Степеневу функцію не важко диференціювати.
Знаходимо диференціал І порядку:

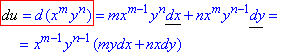
Диференціал II порядку: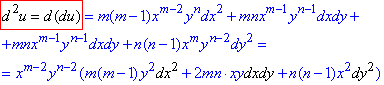

Приклад 1.2 д u=x/y.
Обчислення: Перегляньте, як знаходити диференціали обернених функцій: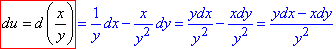

Для порівняння можете зіставити з формулою (5) правил обчислення диференціалів, що наведені на початку уроку в таблиці.
Диференціал II порядку: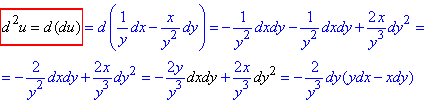

Правила, що тут виділені у формулах Вам допоможуть швидко засвоїти теоретичний матеріал.

Приклад 1.2 u=√(x²+y²).
Обчислення: Диференціал 1 порядку для кореневої функції обчислюємо за формулою 2в: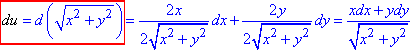

Диференціал 2 порядку: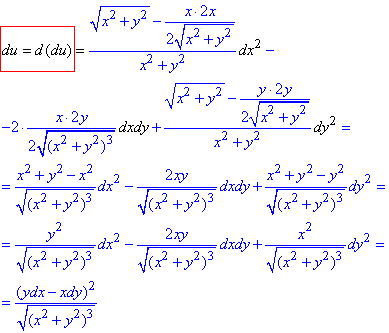

Приклад 1.3 u=exp(xy)
Обчислення: Знаходимо диференціал І порядку від експоненти :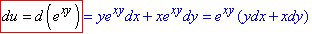

Щоб знати диференціал II порядку повторно диференціюємо du: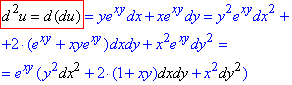

Приклад 1.4 Знайти диференціали першого та другого порядку функції трьох змінних
u=z/(x²+y²).
Обчислення: Диференціал І порядку: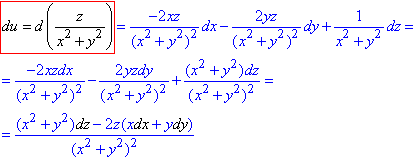

Частинні похідні можна перевіряти в математичних пакетах, зокрема в Мейплі код для похідних за змінними має вигляд:
u := z/(x^2+y^2);
d_x := diff(u, x); d_y := diff(u, y); d_z := diff(u, z);
В результаті отримаємо складові диференціалу першого порядку

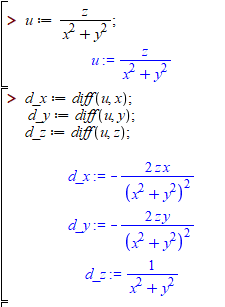
Щоб знайти диференціал II порядку повторно диференціюємо du за трьома змінними, після чого групуємо подібні доданки: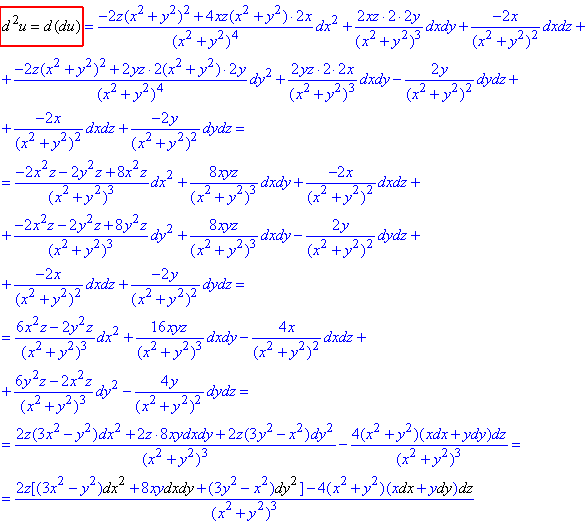

Щоб не помилитись при обчисленні d²u розбийте перший диференціал на три доданки, а далі кожен з них диференціюйте за кожною зі змінних. Після того групуєте доданки при однакових парах dx², dy²,dz²,dxdy, dxdz, dydz.
Ця методика справедлива і для функції багатьох змінних.