Похідні вищих порядків ф-ї двох змінних

Алгоритм обчислення похідних вищих порядків ідентичний до того, що ви робите, щоб знайти часткову похідну першого

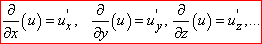
чи другого порядку

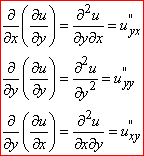
Третя часткова похідна утворюється диференціюванням похідних другого порядку, четверта часткова похідна – обчисленням похідних від похідної 3 порядку за змінними

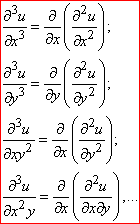
і т. д.
На практиці рідко просять знайти похідні вище 5 порядку, виняток становлять завдання з експонентами та тригонометричними ф-ми, де легко вловити закономірність обчислення похідних.

Почнемо з простіших завдань, які не увійшли до попереднього уроку, а далі важчі.

Приклад 1. Знайти частинні похідні першого та другого порядку
u=cos(x³+y²)
Обчислення: Часткові похідні І порядку:
∂u/∂x=-3x²·sin(x³+y²);
∂u/∂y=-2y·sin(x³+y²).
Часткові похідні ІІ порядку:
∂²u/∂x²=∂u/∂x(-3x²·sin(x³+y²))=
= -6x·sin(x³+y²)-9x⁴·cos(x³+y²);

∂²u/∂y²=∂u/∂y(-2y·sin(x³+y²))=
= -2·sin(x³+y²)-4y²·cos(x³+y²);

∂²u/∂y∂x=∂u/∂y(-3x²·sin(x³+y²))=
= -6yx²·cos(x³+y²).
На сайті постійно вивчаємо математичні пакети, тому покажемо як 1 та 2 часткові похідні обчислювати в мейплі
f := cos(x^3+y^2);
d_x := diff(f, x);
d_y := diff(f, y);
d_xx := diff(f, x, x);
d_yy := diff(f, y, y);
d_xy := diff(f, x, y);

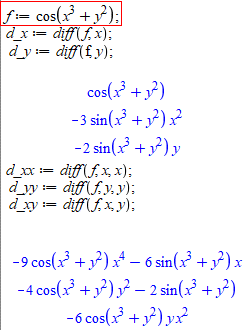
Змінюємо функцію і маємо готовий калькулятор часткових похідних

Приклад 2. Знайти часткові похідні третього порядку ∂³f/∂x³,∂³f/∂y³
f=exp(y+x²)
Обчислення:Експоненту легко як інтегрувати так і диференціювати.
Не забуваємо, що маємо складену функцію та знаходимо часткові похідні 1-3 порядку

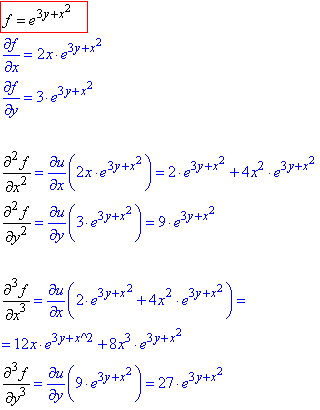
Перевіримо їх в Мейплі, заодно обчислимо мішані похідні третього порядку.
Для цього до вище виписаного коду додамо третю часткову похідну
d_xxx := diff(f, x, x, x);
d_yyx := diff(f, y, y, x);
d_yxx := diff(f, y, x, x);
d_xxx := diff(f, y, y, y)
В результаті отримаємо

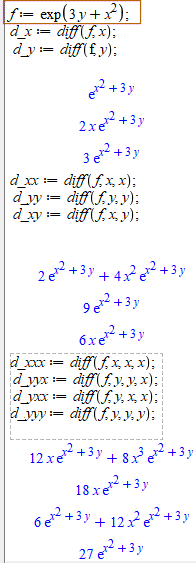
При наборі формул теж слід уважно дивитися, щоб не допустити помилок.

Приклад 3 (2.1) z=ln(x²+xy+y²).
Показати, що має місце рівняння в частвових похідних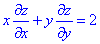

Обчислення: Часткові похідні І порядку: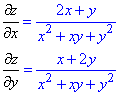

Підставимо отримані похідні у задане диференціальне рівняння: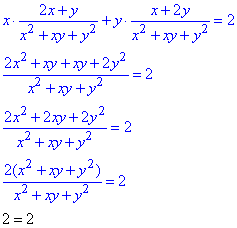

Отримали тотожність, тому задана функція є розв'язком рівняння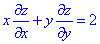

що і треба було довести.

Приклад 4 (4.1) Задана функція двох змінних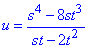

Знайти третю похідну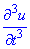 у точці (-1;1).
Обчислення: Часткові похідні І порядку: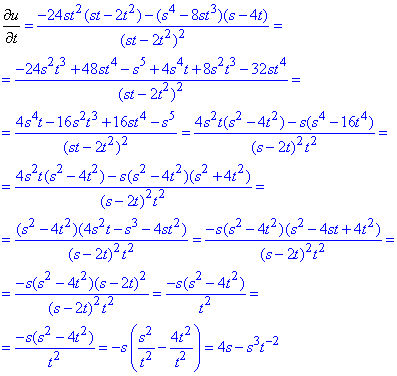

Часткові похідні ІІ порядку: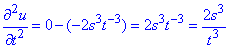

Часткові похідні ІІІ порядку: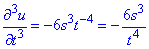

Обчислимо часткову похідну 3 порядку у точці (-1;1).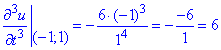

Якщо попередньо спростити вираз функції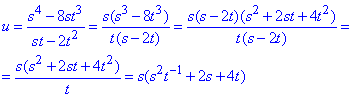

то відшукання часткової похідної І порядку стає легким.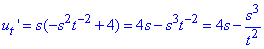

Відповідно і похідні вищих порядків легше знаходити.

Приклад 5 (4.2) z=x⁴+x³y+x²y²+xy³+y⁴.
Знайти частинні похідні четвертого порядку.
Обчислення: У функціях подібного виду похідна вищого порядку береться лише від виразів, у яких змінні мають степінь не нижче порядку похідної по кожній змінній, решта – нулі, оскільки на певних етапах вони стають константами, а похідна від сталої рівна 0.
Знаючи це правило, можемо записати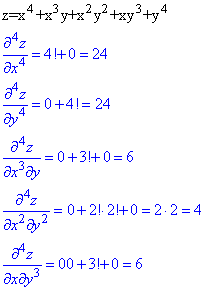

Спробуйте перевірити самостійно.

Приклад 6 (4.3) Знайти четверті похідні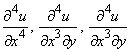

якщо функція має вигляд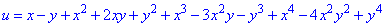

Обчислення: Нагадуємо правило, що у многочленах з кількома змінними похідна вищого порядку береться лише для виразів, змінні яких мають степінь, який рівний або вище порядку похідної по кожній змінній, решта – нулі. Це тому, що після ряду диференціювань залишаються тільки сталі.
Тому аналізуючи вигляд ф-ї, отримаємо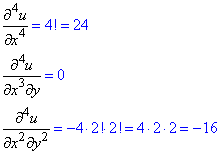

Для перевірки розв'яжіть це завдання самостійно.