Диференціали вищих порядків функцій двох змінних + приклади

Повторимо формули, як обчислювати диференціали першого та другого порядку для функції двох та трьох змінних, що були наведені на попередньому уроці та перейдемо до обчислення диференціалів вищих порядків.

Якщо задана диференційовна функція трьох змінних u=f(x;y;z) то повний диференціал обчислюють за формулами:

Диференціал І порядку
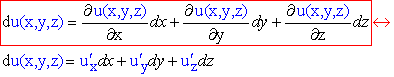(1)
Диференціал II порядку та старших
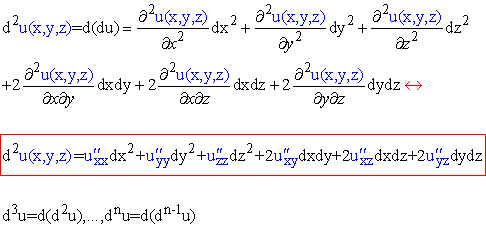(2)
Як знайти частинні похідні вчили на попередніх уроках і продовжимо тут, це всього навсього звичайні похідні за конкретними змінними, при цьому решту змінних в функції вважаємо незалежними від тієї, по якій обчислюємо похідну.

Формули повних диференціалів для функції двох змінних u=f(x, y):
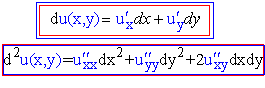(3)

Оскільки для обчислення диференціалів вищих порядків необхідно знайти диференціал на порядок нижче
dⁿu=d(d^n-1u), (4)
то і перший і другий диференціали будемо тут знаходити.
Наведемо формули основних диференціалів, щоб постійно не звертатися до таблиці похідних

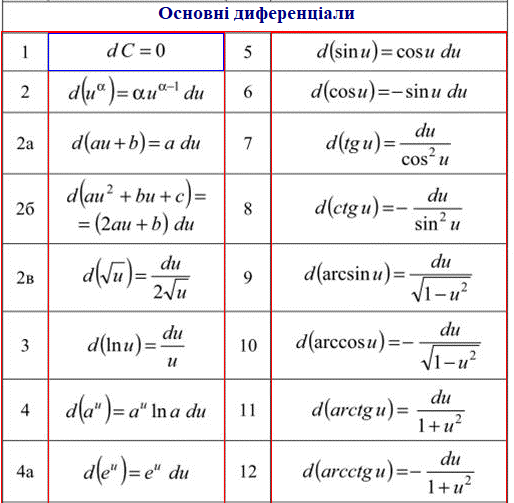
Переходимо до практичних з яких навчимося, як знайти повний диференціал другого та вищих порядків.

Приклад 2.1 Обчислити перший та другий диференціали
u=cos(x+y²)
Обчислення: За формулою (6) таблиці основних диференціалів розписуємо
du=d(cos(x+y²))=-sin(x+y²)d(x+y²)=-sin(x+y²)dx-2y∙sin(x+y²)dy.
Щоб знайти другий диференціал застосовуємо формулу (3)
d²u=-cos(x+y²)dx²-4y∙cos(x+y²)dxdy-4y²∙cos(x+y²)dy²

Приклад 2.2 Знайти диференціал третього порядку d³u, якщо u=x³+y³-3xy(x-y)

Обчислення: Розпишемо функцію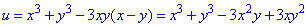

Складемо диференціал І порядку за формулою (3):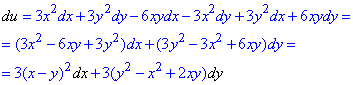

Диференціал II порядку: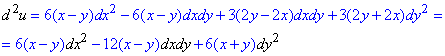

Обчислення: Диференціал IIІ порядку: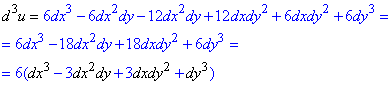

Приклад 2.3 Обчислити десятий диференціал d¹⁰u, якщо u=ln(x+y)
Обчислення: Диференціал І порядку: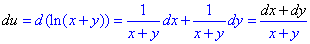

Диференціал II порядку: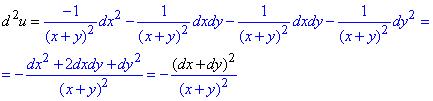

Диференціал IIІ порядку: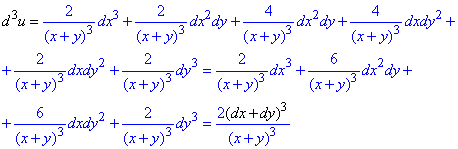

Аналізуючи формули диференціалів першого - третього порядку вловлюємо закономірність, яка дозволяє виписати формулу
диференціалу IV порядку: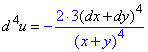

та старших.
Диференціал n-го порядку: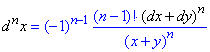

Звідси диференціал X порядку: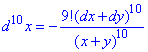

Приклад 2.4 Знайти третій диференціал d³u, якщо u=xyz.
Обчислення: Диференціал І порядку:

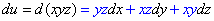
Диференціал ІI порядку: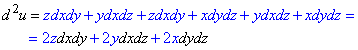

Диференціал ІII порядку: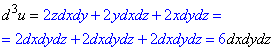

Приклад 2.5 Визначити dⁿu, якщо u=exp(a∙x+b∙y).
Обчислення: Диференціал І порядку: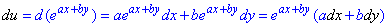

Диференціал ІI порядку: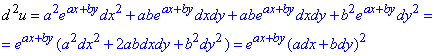

Диференціал ІII порядку: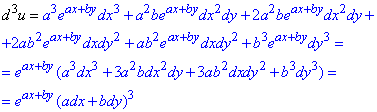

Диференціал n-го порядку: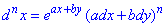

Якщо маєте труднощі з обчисленням повних диференціалів другого чи вищих порядків, не знаєте як знайти похідні складених функцій, можете звертатись за допомогою або консультацією.
На практичних Вам потрібно знати або мати перед очима таблиці похідних, далі вміти їх застосувати для обчислення частинних похідних, а вже скласти формулу деренціалів функцій не важко.