Часткова похідні І та ІІ порядку функції двох змінних

Часткова похідна першого порядку функції багатьох змінних u(x;y;z,…) обчислюється за правилами, як і звичайна похідна для функції однієї змінної.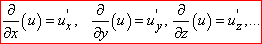

При обчисленні похідних інші змінні не залежать від тієї по якій диференціюємо, і так для кожної змінної.
Частковими похідними другого порядку функції двох змінних u(x;y) називається їх часткові похідні від часткових похідних першого порядку.
Позначення других часткових похідних: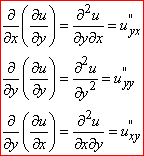

Для функції трьох змінних до цих формул добавиться друга похідна по z та дві мішані похідні по xz та yz.
Аналогічно визначаються похідні вищих порядків, наприклад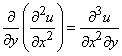

і т.д.
Частинні похідні, які відмінні одна від одної лише порядком диференціювання, називаються мішаними похідними;
вони є рівними між собою при умові, що неперервні в деякому околі точки M.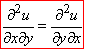

Далі наведемо приклади з практики студентів, які Вас можуть чекати. Перегляньте обчислення та оформлення завдань на похідні функцій u(x;y).

Знайти часткові похідні першого і другого порядку функції двох змінних

Приклад 1. u=x⁴+y⁴-4x²y².
Обчислення: Пояснювати, як брати похідні тут не будемо. Для цього на сайті є окремий розділ, який вчить знаходити похідні.
Знаходимо часткові похідні І порядку: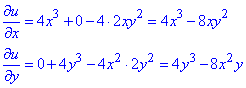

Часткові похідні II порядку: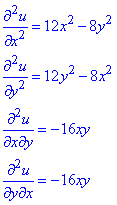

Оскільки сама функція u(x;y) і її часткові похідні першого порядку неперервні на всій області визначення, то мішані похідні рівні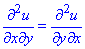

.

Приклад 2. u=x/y².
Обчислення: Часткові похідні І порядку: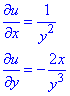

Часткові похідні II порядку: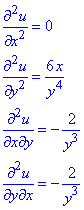

Мішані похідні співпадають, оскільки функція u(x,y) з її похідними першого порядку неперервна на всій області визначення.
Ви можете заперечувати таз огляду на вигляд u=x/y² стверджувати, що функція розривна при y=0, але ця точка не входить в область визначення, а всюди поза точкою ф-я неперервна і диференційовна.

Приклад 3. u=x•sin(x+y).
Обчислення: Часткові похідні І порядку: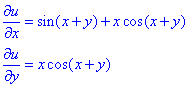

Часткові похідні II порядку: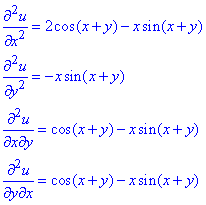

Мішані похідні рівні між собою.

Приклад 4. u=tan(x²/y²).
Обчислення: Уважно перегляньте правила похідних від складених функцій, це спростить обчислення цього та наступних за ним прикладів.
Часткові похідні І порядку: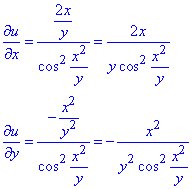

Часткові похідні II порядку: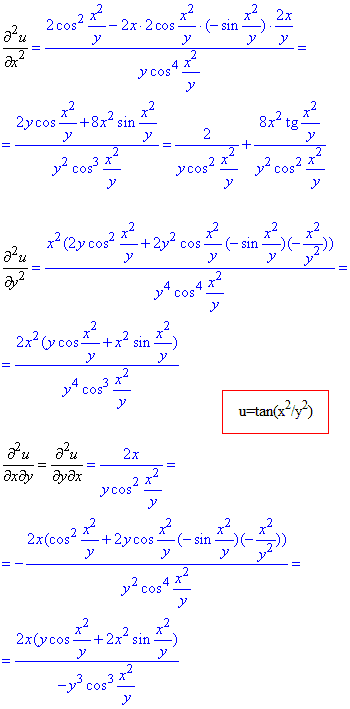

Приклад 5. u=ln(x+y²).
Обчислення: Часткові похідні І порядку: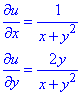

Часткові похідні II порядку: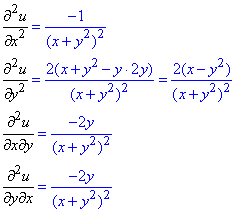

Як бачимо мішані похідні співпадають.

Приклад 6.Знайти похідні першого та другого порядку функції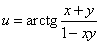

Обчислення: Часткові похідні І порядку: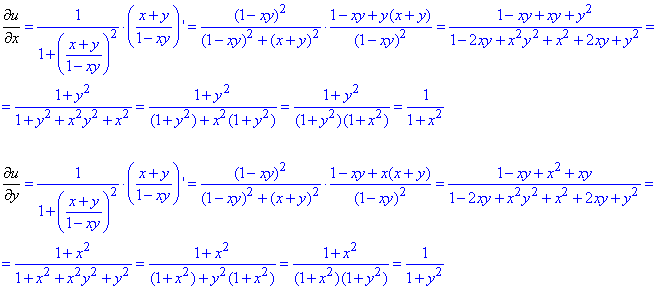

Часткові похідні II порядку: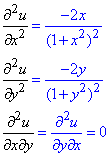

Часткові похідні І порядку можна віднайти набагато легше, якщо впізнати формулу з обернених тригонометричних функцій: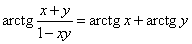

Приклад 7 (2.2) T=π√(l/g). Показати, що

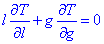
Обчислення: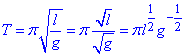

Знаходимо часткові похідні І порядку: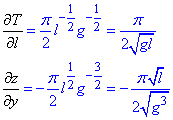

Підставимо отримані похідні у задане диференціальне рівняння: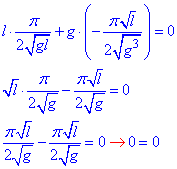

Отримали тотожність, тому задана функція 1 є розв'язком рівняння 2.

Приклад 8 (3.1) {x=ρ•cos(φ), y=ρ•sin(φ)}.
Обчислити визначник складений з часткових похідних

Обчислення: Визначаємо часткові похідні І порядку: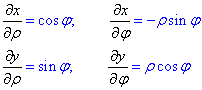

Підставимо отримані похідні у заданий визначник і обчислимо його: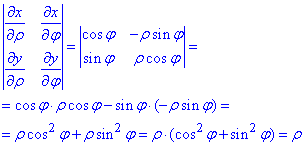

Цей визначник є якобіаном переходу від декартових до полярних координат, і його неодноразово будете бачити в інтегруванні.

Приклад 9. Знайти часткові похідні I та II порядку.
u=1/√(x²+y²+z²).
Обчислення:Спершу перетворимо функцію для зручності брати похідну

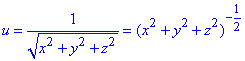
Знаходимо часткові похідні І порядку за правилом похідної складеної функції: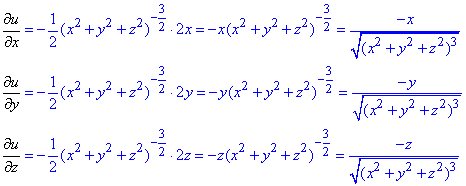

Далі часткові похідні II порядку: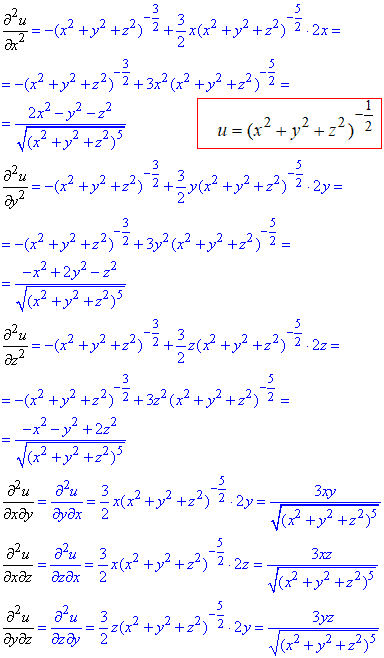

З коренями не всім легко даються похідні, тому будьте уважні при обчисленнях.

Приклад 10. Знайти перші та друг часткові похідні
u=x^(y/z).
Обчислення: Часткові похідні І порядку: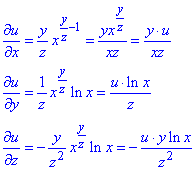

Часткові похідні II порядку: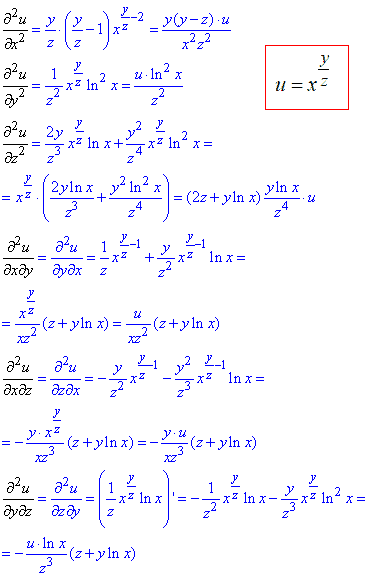

Часткові похідні потрібні для дослідження функцій багатьох змінних, пошуку точок екстремуму, перегинів, обчислення диференціалів, значення похідних в точці.
Все поступово навчимося виконувати з наступних уроків.