Поверхні рівня функції+Приклади

Поверхнею рівня називають такі поверхні, в кожній точці яких функція u=f(x,y,z) трьох координат (змінних) має однакове значення
f(x,y,z)=C=const.

На практиці визначення поверхні рівня зводиться до прирівняння функції трьох змінних до сталої, далі, якщо є можливо, вираженні однієї з координат через дві інші та сталу. В загальному поверхня рівня – це просторовий об'єкт і лише в часткових випадках отримаємо площини.
На практичних, особливо де потрібно побудувати графік поверхні рівня, Вам не задаватимуть чогось надзвичайного.
Достатьно знати рівняння площини та кілька фігур обертання, зокрема як будувати сферу, циліндр, конус (гіперболоїд, параболоїд, тор).
В природі до поверхонь рівня відносяться поверхні рівної температури, рівного тиску, вологості. Наприклад для краплі води поверхнею рівня буде поверхня, що межує з повітрям (форма каплі, що бачимо).

Приклад 1. Побудувати поверхні рівня функції
u=x+y+z.
Розв'язування: Виписуємо рівняння поверхні рівня
x+y+z=c.
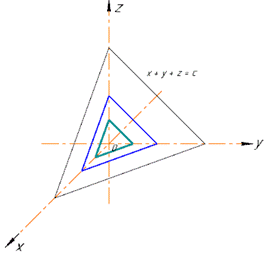
При зміні сталої отримаємо множину паралельних площин, рівнонахилених до напрямку координатних осей.
Схематично покажемо, як перетинають ці поверхні координатні площини.

Приклад 2. u=x^2+y^2-z^2.
Розв'язування: Записуємо рівняння повехні рівня
x²+y²-z²=c.
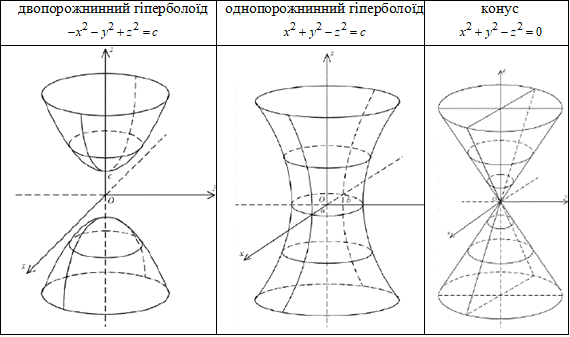
Отримали множину двопорожнинних гіперболоїдів при u<0;
множину однопорожнинних гіперболоїдів при u>0;
конус при u=0.
Таблицю з рисунками можливих поверхонь рівня наведено нижче

Приклад 3. Визначити поверхню рівня функції
u=(x-5)²+(y-3)²+(z-7)².
Розв'язування: Складаємо рівняння поверхні рівня
(x-5)²+(y-3)²+(z-7)²=c.
З рівняння бачимо, що це множина концентричних сфер з центром в точці (5;3;7).

Приклад 4. Cкласти поверхню рівня та визначити її вигляд
u=(x+y)²+z².
Розв'язування: За наведеним вище алгоритмом записуємо
(x+y)²+z²=c
Формула описує множину еліптичних циліндрів, спільною віссю яких є пряма x+y=0, z=0.

Приклад 5. Побудувати поверхню рівня функції
u=z-ln(x+y)·(x²-y).
Розв'язування: Прирівнюємо праву сторону до сталої
z-ln(x+y)·(x²-y)=c.
При с=0 будемо мати 
z=ln(x+y)·(x²-y)
Побудуємо поверхню рівня в Мейплі
plot3d(ln(x+y)*(x^2-y), x = 0 .. 5, y = 0 .. 6) ;

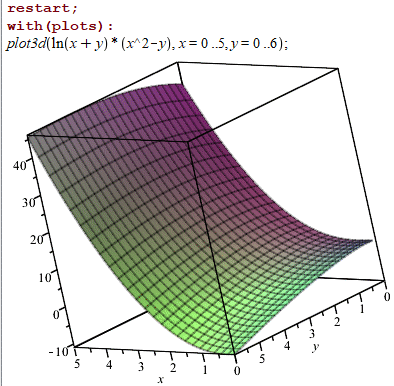
При інших сталих c поверхня буде зміщатися вгору або вниз по осі Oz.

Подібних прикладів можна привести безліч, Вам головне з уроку знати, що таке поверхня рівня, і уявляти як геометрично виглядають простіші із них.