Сьогодні розглянемо завдання де потрібно зробити перехід від одних змінних до інших для функції двох змінних. Аглоритми, що тут розглянуті є універсальними і Ви їх повторно навчитеся застосовувати до інших подібних прикладів, що Вам задають.
Приклад 1. Знайти f(1,y/x), якщо f(x,y)=2xy/(x2+y2)
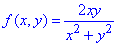
Розв'язування: Нехай маємо
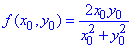
Тоді за умовою, замінюємо першу координату на x0=1, другу – на y0=y/x.
Отримаємо:
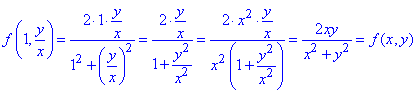
Думаю такий тип завдань Ви зможете виконати самостійно.
Приклад 2. Нехай z=√y+f(√x-1)
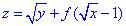
Знайти функції f і z, якщо z=x при y=1.
Розв'язування: Перегляньте прийоми викорастані для вираження функції f(x).
Підставимо в рівняння
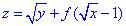
значенння з умови z=x при y=1.
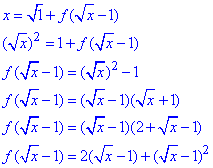
переходячи до нової змінної t=√x-1, отримаємо
f(t)=2t+t2.
Враховуючи умову z=√y+f(√x-1) і нову зміну t=√x-1, запишемо
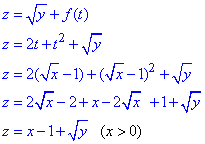
Приклад 3. Знайти f(x,y), якщо f(x+y,y/x)=x2-y2.
Розв'язування: Виконаємо певні маніпуляції зі змінними, щоб перейти до потрібних
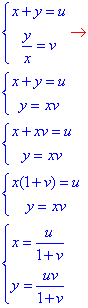
Підставимо отримані вирази в задану функцію:
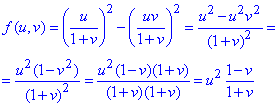
Переходячи до змінних x і y, отримаємо остаточно
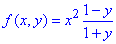
Всіх перетворень тут не виписували, тому переконайтесь самостійно, що кінцева формула буде такою.
Приклад 4. Знайти f(x), якщо f(y/x)
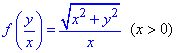
Розв'язування: Виконуємо елементарні перетворення в правій частині, щоб добитися вигляду функції від y/x:
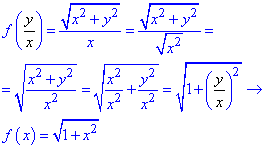
Приклад 5. Нехай z=x+y+f(x-y).
Знайти функції f і z, якщо z=x^2 при y=0.
Розв'язування: Підставимо значення з умови в функцію
x2=x+0+f(x-0),
звідси f(x)=x2-x.
Враховуючи умову z=x+y+f(x-y), запишемо
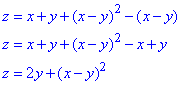
Подібні приклади Ви не один раз зустрінете при вивченні функцій багатьох змінних. Які заміни змінних чи переходи слід виконувати ми тут розглянули. Єдине, що можемо порадити, вчіться розв'язувати самостійно.
Лише перечитуванням готових розв'язків Ви успіху в математиці не досягнете!

