Похідна неявно заданої функції + Приклади

Нехай неперервна функція y від х задається неявним рівнянням F(x;y)=0, де F(x;y), F'_x(x;y), F'_y(x;y) - неперервні функції в деякій області D, що містить точку (x;y), координати якої задовольняють дане рівняння;
крім цього, в цій точці F'_y(x;y)≠0.
Тоді похідна y від x:
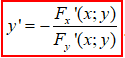(1)
Для відшукання часткових похідних ∂z/∂x, ∂z/∂x від функції F(x;y;z) мають місце наступні формули:
(2)

На попередньому уроці вчили знаходити похідні складених функцій 2, 3 змінних і таблиця похідних була потрібна. Цього разу тема дещо легша, але таблицю похідних продовжимо вивчати та застосовувати.

Приклад 3.1 Знайти похідну dy/dx від функцій, заданих рівнянням
x²y+xy²-y³-1=0.
Обчислення: Похідні неявних функцій будемо визначати за (1) формулою, тому спершу записуємо неявне рівняння як функцію, далі беремо часткові похідні та застосовуємо формулу (виділена прямокутником).

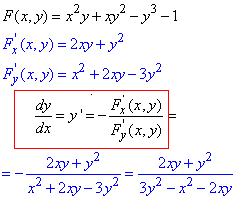
Як Ви могли переконатися, це легші завдання в порівнянні з параметрично заданими функціями.

Приклад 3.2 Знайти похідну dy/dx неявно заданої функції
x∙e^y+y∙e^x-e^xy=0.
Обчислення: Повторюємо алгоритм похідної неявної функції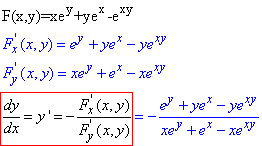

Тут більше спрощувати немає чого.

Приклад 3.3 Знайти похідну dy/dx функції
x^2/3+y^2/3=a^2/3.
Обчислення: Переносимо сталу за знак рівності та застосовуємо формули похідної для неявно заданої функції та (8) з таблиці похідних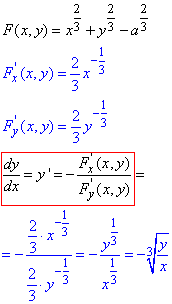

У Вас може виникнути запитання, чому формули робимо не широкими?
Відповідь наступна: оскільки значна частина аудиторії сайту заходить з мобільних пристроїв, а для них важливо, щоб формули вміщалися на екрані та були читабельними, то їх мінімізуємо по ширині де це є можливо.

Приклад 3.4 Визначити похідну dy/dx неявної функції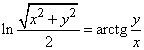

Обчислення: За методикою переносимо все в одну сторону від знаку рівності, пригадуємо похідну логарифма (13) та арктангенса (22) і обчислюємо, при цьому не забуваємо що обидві функції є складеними (множимо на похідну аргументу за змінними)

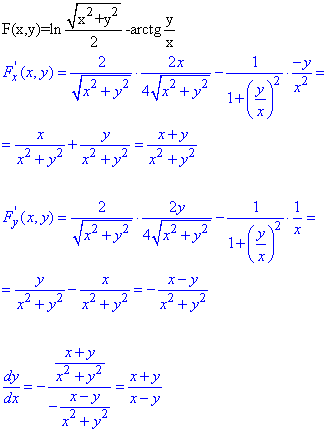
Друга похідна неявно заданої функції

Приклад 4.1 Обчислити другу похіднуy''
x²+2xy-y²=a².
Обчислення: Першу похідну знаходимо за правилом для неявних функцій. Після того як ми маємо похідну в явному вигляді, то друга похідна неявної функції рівна похідній від обчисленої похідної. Нам не потрібно застосовувати правило для неявних ф-й двічі.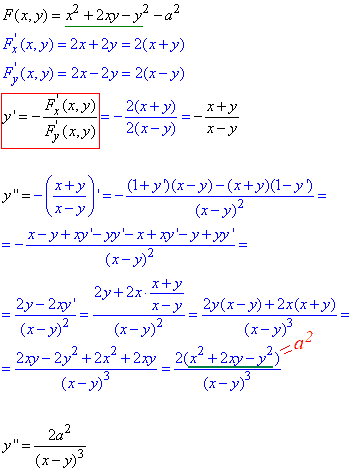

Вкінці розрахунків в чисельнику отримали вираз, що містить початково задану функцію, тому результат спростили.

Приклад 4.2 Знайти другу похідну y''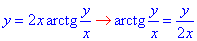

Обчислення: Знову маємо неявно задану функцію, тому в умові зразу виконали певні перетворення, які при обчисленнях зведуть неявну похідну до компактного запису. Далі другу похідну знаходимо як похідну похідної.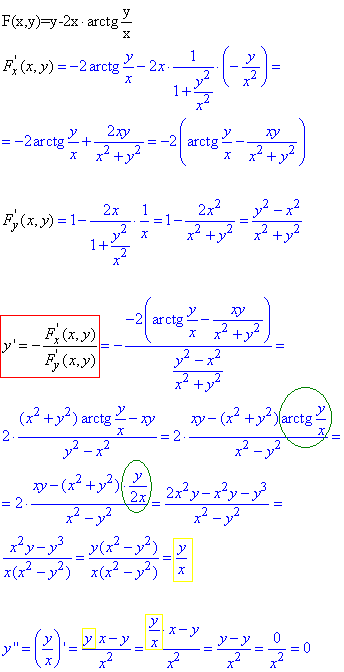

Попереду Вас чекають готові приклади на границі функцій багатьох змінних, пошук точок та характеру екстремуму, градієнту і ще багато чого з того, що Вас вчитимуть в курсі математичного аналізу.