Наближені обчислення за допомогою диференціалу

Нехай задано диференційовну в точці (x, y, z) функцію трьох координат z=f(x, y, z).
Випишемо її повний приріст:
Δz=f(x+Δx, y+Δy, z+Δz)-f(x, y, z)
Звідси
f(x+Δx, y+Δy, z+Δz)=f(x, y, z)+Δz. (1)
Запишемо приріст функції Δz через диференціали:

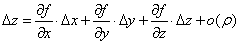
Якщо в прирості Δz відкинуті малі величини та підставити в (1) то отримаємо формулу наближень
(2)
Це і є розрахункова формула для наближених обчислень значень функцій в точці z=f(x+Δx, y+Δy, z+Δz).

Добуток часткової похідної ∂u/∂x на довільний приріст Δx називається частковим диференціалом по x функції, і позначають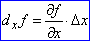

Якщо задана диференційована функція двох координат z=u(x, y) то формула наближених обчислень приросту через повний диференціал має вигляд:
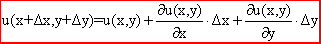(3)

Наближені обчислення значень функції

Приклад 1. Знайти значення √26
Розв'язування: Почнемо з простішого одномірного випадку, щоб Ви зрозуміли наскільки ця методика проста і ефективна.
Знаходимо найбільше ціле число, квадрат якого не перевершує 26.
Це буде 25.
Далі число 26 подамо як 25+1, тоді x₀=25, Δx=1.
Коренева функція y=√x в точці х₀ рівна
y(x₀)=√25 =5.
Диференціал в точці x₀:
d[y(x₀)]=y'(x₀)•Δx.
Знайдемо його

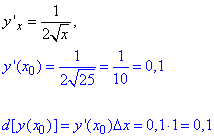
За наближеною формулою
y(x₀+Δx)≈y(x₀)+d[y(x₀)]=y(x₀)+y'(x₀)•Δx
y(26)=5+0,1=5,1.
Точне значення кореня з 26 рівне
y(26)=√26≈5,0990195
Чим менше Δx, тим формула наближень дає меншу похибку.

Приклад 2. За допомогою диференціала знайти

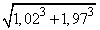
Розв'язування: Пригадуємо формулу наближених обчислень для функції двох змінних і розписуємо підкореневий вираз у вигляді суми початкового значення та приростів

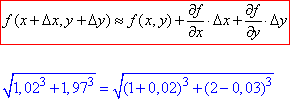
Звідси виписуємо початкове наближення x₀=1, y₀=2, та дельти Δx=0,02, Δy=-0.03.
Подано функцію, що наближаємо у вигляді
f(x, y)=√(х³+y³)
та знайдемо значення в точці (x₀;y₀):

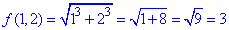
Знайдемо часткові похідні І порядку у точці (1;2):

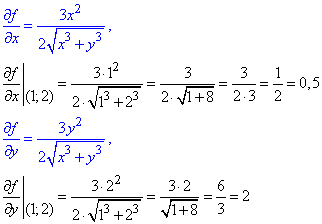
Обчислимо наближено заданий корінь:

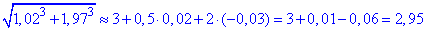
Точне значення кореня виразу 2,9506916.
Бачимо, що з точністю до тисячних обчислення вірні.

Приклад 3 Знайти наближене значення кореня

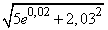
Розв'язування: Виписуємо корінь квадратний через прирости

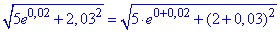
звідси x=0, y=2, Δx=0,02, Δy=-0.03.
Функція, якою наближаємо:
f(x, y)=√(5e^x+y²)
Знайдемо початкове наближення

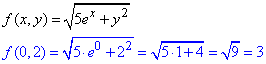
Обчислюємо часткові похідні І порядку у точці (0;2):

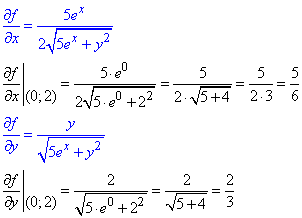
Далі через диференціал наближено знаходимо значення кореня:

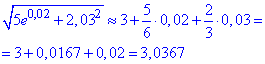
Точне значення 3,036759.

Приклад 4. Обчислити наближено за допомогою диференціала

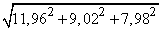
Розв'язування: Не важко догадатися, що функція для наближення наступна:
f(x, y)=√(x²+y²+z²)
Подаємо корінь з трьох доданків через прирости

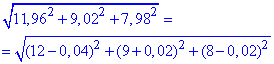
звідси початкове значення x=12, y=9, z=8, та дельти Δx=-0,04, Δy=0,02,Δz=-0,02.
Обчислюємо початкове наближення функції

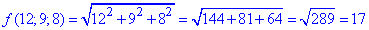
Визначаємо часткові похідні першого порядку у точці (12;9;8) :

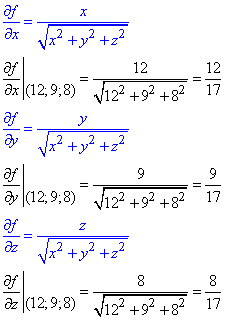
Знайдені часткові диференціали в точці підставляємо в формулу наближених обчислень:

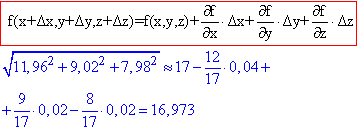
Точне значення кореня 16,97299.

Приклад 5. Обчислити значеня кореня

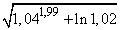
Розв'язування: Наближати будемо за допомогою функції
f(x, y)=√(x^y+ln(z))
Перепишемо корінь квадратний у приростах

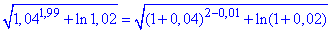
звідси x=1, y=2, z=1, Δx=0,04, Δy=-0,01,Δz=0,02.
Знаходимо нульове наближення

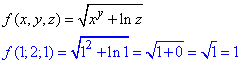
Обчислюємо часткові похідні функції в точці (1;2;1):

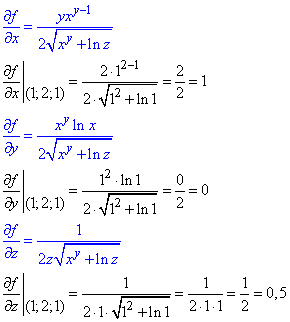
Застосовуємо формулу наближених обчислень:


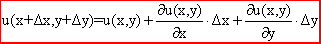
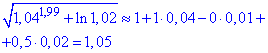
Точне значення 1,049275.
Великої похибки обчислень не слід було чекати, оскільки відхилення від початкового наближення малі.
Для закріплення матеріалу самостійно обчисліть наближені значення виразів

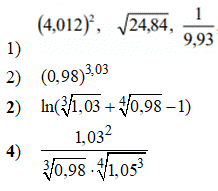
Застосовуйте наведений алгоритм обчислення наближеного значення функцій до задач, що задають на практичних. Розрахунки не важкі, як знайти часткові диференціали чи похідні неодноразово бачили як на цьому уроці, так і на попередніх. Вчіть таблицю похідних, без вміння нею користуватися буде не просто при вивченні багатьох тем з мат. аналізу.