Якщо кожній парі (x;y) значень двох, незалежних один від одного, змінних величин x і y, із деякої області їх змінення D, відповідає єдине значення величини z, то говорять, що z є функція двох незалежних змінних x і y, що визначена в області D.
Позначення: z=f(x, y).
Сукупність пар (x;y) значень x і y, за яких визначається функція z=f(x;y), називається областю визначення, або областю існування цієї функції.
Геометричне місце точок, координати яких задовольняють рівнянню z=f(x;y), називається графіком функцій двох змінних.
Якщо кожній розглядуваній сукупності значень змінних x, y, z, …, u, t із деякої області D (області визначення функції) відповідає єдине значення змінної w, то говорять, що w є функція багатьох незалежних зміннихx, y, z, …, u, t.
Позначення: w=f(x, y, z, …, u, t).
наприклад w=f(x;y;z) - функція трьох змінних і т.д.
Розглянемо точки області D, в яких функція u=f(x;y;z) має постійне значення:
f(x;y;z)=c.
Сукупність цих точок утворює деяку поверхню.
Якщо візьмемо інше значення c, то отримаємо другу поверхню.
Ці поверхні називаються поверхнями рівня.
Якщо функція u є функцією двох змінних x і y, тобто u=f(x;y), то "поверхнями" рівня будуть лінії на площині:
f(x;y)=c, які називаються лініями рівня.
Якщо значення u ми будемо відкладати по осі : z=f(x;y)
то лініями рівня на площині Oxy будуть проекції ліній, які отримуються в перетині поверхні z=f(x;y) з площинами z=c (рис. 1).
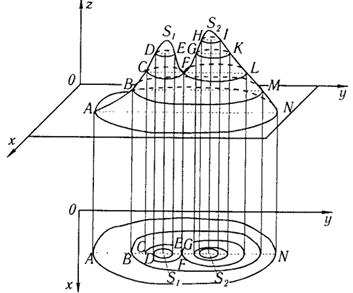
Визначити та зобразити області існування функцій
Приклад 1. u=x+√y.
Розв'язування: Оскільки під коренем парного степеня функція набуває невід'ємних значень, то y≥0, тому область існування функції є вся півплощина, що знаходиться вище осі Oy, включаючи й саму вісь.
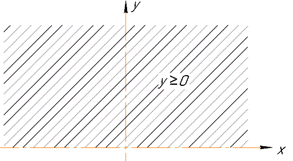
Приклад 2 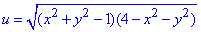
Розв'язування:Маємо кореневу функцію двох змінних, записуємо умову, що множники під коренем приймають невід'ємні значення та розкриваємо відповідні нерівності
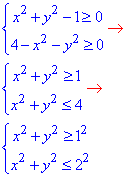
Областю визначення u(x, y) є кільце, що обмежене колами з радіусами R=1 і R=2.
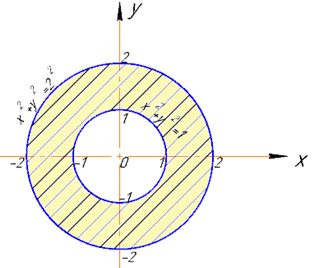
Межі входять в область.
Приклад 3 Знайти та побудувати область визначення u(x, y)
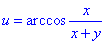
Розв'язування: Арккосинус - обернена тригонометрична функція, що визначена на проміжку [-1;1].
Тому і вираз під арккосинусом має змінюватися в цьому діапазоні. Крім цього знаменник дробу не повинен перетворюватися в0.
Складаємо систему нерівностей
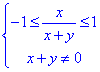
розділяємо її на дві підсистеми
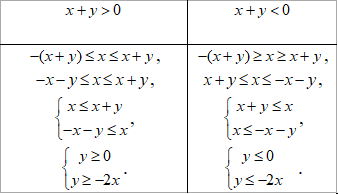
Отримали пару вертикальних тупих кутів, які обмежені прямими y=0 і y=-2x, включаючи цю межу без спільної вершини (0;0).
Будуємо область існування функції u=arccos(x/(x+y)) графічно
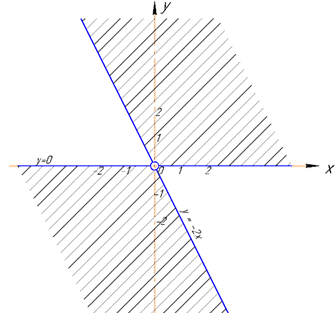
Початок координат не входить в область визначення тому що маємо умову x+y≠0.
Приклад 4 Зобразити область визначення функції трьох змінних
u=ln(1-x2-y2+z2).
Розв'язування: Логарифмічна функція визначена для змінних більших нуля, тому розписуємо відповідну нерівність:
-1-x^2-y^2+z^2>0,
х^2+y^2-z^2<-1.
отримали внутрішність двопорожнинного гіперболоїда.
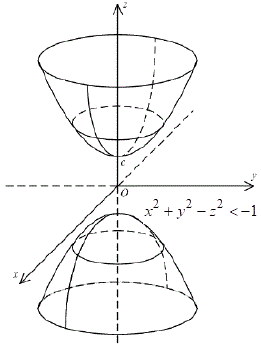
(Збірник задач Б. П. Демидович)
Приклад 5. (3139) Побудувати область існування функції
u=1//√(x2+y2-1).
Розв'язування: Оскільки під коренем парного степеня функція набуває невід'ємних значень, то
x2+y2-1≥0,
x2+y2≥1,
тому область існування функції є зовнішність кола з центром (0;0) та радіусом R=1.
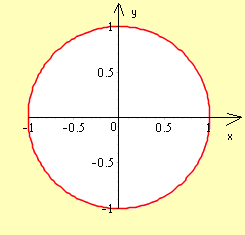
Приклад 6. (3142) Якими кривими обмежена область визначення функції
u=√(1-(x2+y)2).
Розв'язування: Підкоренева функція не повинна приймати від'ємних значень.
З цієї умови отримуємо та розписуємо нерівність.
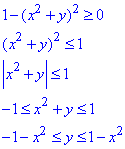
Отримали множину точок площини, яка обмежена параболами y=1-x2 і y=-1-x2.
Приклад 7. (3144)Записати нерівності, що визначають область визначення функції
u=arcsin(y/x).
Розв'язування:Арксинус визначений для аргументів, які за модулем не перевищують одиниці. Крім того, маємо дробову функцію під арксинусом, тому накладаємо додаткову умову на знаменник x≠0.
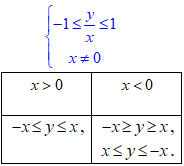
Аналізуючи нерівності, приходимо до висновку, що область існування обмежена парою вертикальних кутів |y|≤|x| (x≠0).
Приклад 8. (3148) Знайти область визначення функції трьох змінних
u=arcos(z/√(x^2+y^2).
Розв'язування:Складаємо систему нерівностей з обмеження на арксинус та знаменник дробу
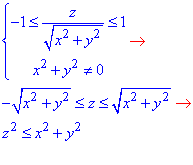
Нерівність z2≤x2+y2 описує зовнішність конуса x2+y2=z2, включаючи межу за виключенням самої вершини (0;0;0).
Далі навчимося будувати лінії та поверхні рівня, знаходити границі та похідні функцій багатьох змінних.

