Найбільше та найменше значення функції багатьох змінних в замкненій області

Як знайти найбільше та найменше значення z=f(x, y) в замкненій області?

Для знаходження мінімуму максимуму диференційовної функції в замкненій та обмеженій області D, потрібно:
1) знайти критичні точки, що належать області D, і обчислити значення функції у цих точках;
2) знайти найбільше та найменше значення функції на лініях, які утворюють межу області;
3) з усіх знайдених значень вибрати найбільше та найменше.
Наведений спосіб встановлення мінімуму (максимуму) функції двох змінних в замкненій області, ще називають методом підстановки.
Чому саме так і як це виглядає на практиці ми зараз розберемо на кількох завданнях.

Приклад 1. Знайти найбільше та найменше значення функції z(x,y)=x²-y² в крузі x²+y²≤4.
Розв'язування: Знайдемо часткові похідні першого порядку заданої функції:
z'_x=2x, z'_y=-2y.
Прирівняємо до нуля отримані вирази, щоб знайти критичні точки:
z'_x=0, z'_y=0;
2x=0, -2y=0;
x=0,y=0.
M(0;0).
Дослідимо поведінку функції z=x^2-y^2 на межі області (круга x²+y²≤4):
Всюди, де область в якій досліджуємо функцію можна зобразити, робіть схематичний рисунок

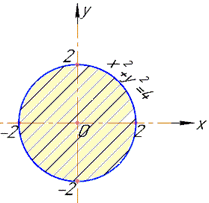
З рівняння круга виражаємо одну зі змінних y²=4-x², та підставляємо в формулу функції

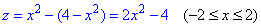
Прирівнюємо похідну z' до нуля і знаходимо критичні точки
z'=(2x²-4)'=4x=0,
отримаємо x=0, тоді y1=2, y2=-2.
Далі виражаємо змінну "ікс" з рівняння границі:
x²=4-y², звідси

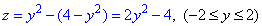
z'=(2y²-4)'=4y=0, отримаємо y=0, отже x1=2, x2=-2.

Знайдемо значення функції у критичній точці (0;0) та у точках на межі області (0;2), (0;-2) і (2;0), (-2;0):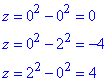

Отримали:
z_min=-4 - найменше значення в точках (0;-2), (0;2);
z_max=4 - найбільше значення в точках (-2;0), (2;0).
Для наочності побудуємо тримірний рисунок функції двох змінних в області дослідження - крузі/
Скористаємося математичним пакетом Мейпл:
with(plots):
plot3d(x^2-y^2, x = -sqrt(4-y^2) .. sqrt(4-y^2), y = -2 .. 2);
В результаті отримаємо 3D просторової функції, який можна обертати в трьох осях.
Далі перетворили його в анімацію

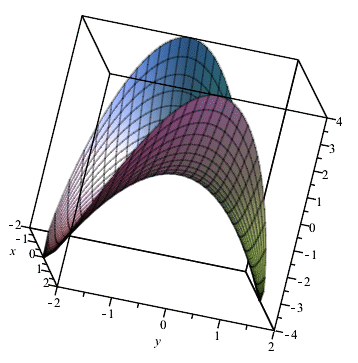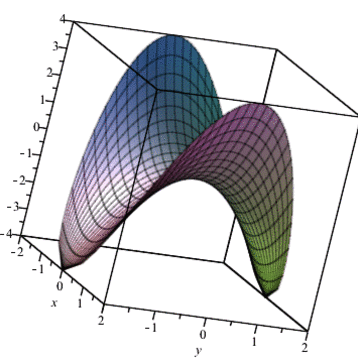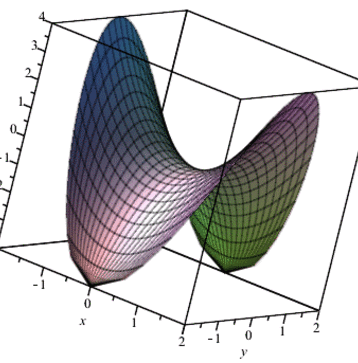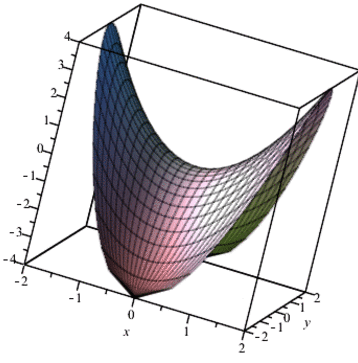
Приклад 2. Знайти мінімум максимум функції z=x²-xy+y²-4x у замкненій області, обмеженій прямими x=0, y=0, 2x+3y-12=0.
Розв'язування: Знайдемо часткові похідні першого порядку заданої функції:
z'_x=2x-y-4,
z'_y=-x+2y.
Прирівняємо до нуля отримані вирази:

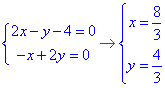
Знайдемо поведінку функції на межі області, обмеженій прямими x=0, y=0, 2x+3y-12=0.
Побудувавши прямі, отримаємо трикутник

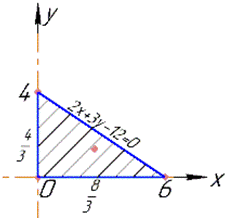
I. На прямій 2x+3y-12=0 виражаємо "ікс" x=6-1,5y та підставляємо в функцію

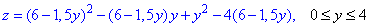
далі знаходимо часткові похідні та з умови їх рівності нулю визначаємо критичну точку

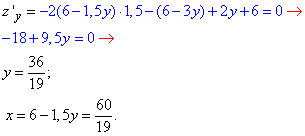
II. Аналогічно: з умови 2x+3y-12=0 виражаємо "ігрик" y=4-2/3*x та підставляємо в z(x, y):

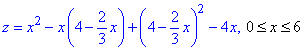
Далі визначаємо критичні точки

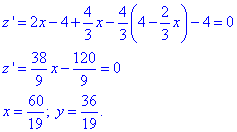
III. Ще дві точки знайдемо з умови перетину прямих з умови:
1) x=0, 2x+3y-12=0:
3y-12=0, y=12/3=4. A(0;4);
2) y=0, 2x+3y-12=0:
2x-12=0, x=12/2=6. A(6;0).
Не забувайте виписувати та перевіряти наведені точки на локальний екстремум.
Обчислимо значення функції у критичній точці (8/3;4/3)
та у точках на межі області (0;4), (6;0), (0;0), (60/19;36/19)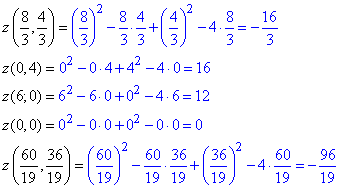

Отримали:
в точці M(8/3;4/3) функція досягає мінімального значення z_min=-16/3 в області
в M1(0;4) функція досягає максимуму z_max=16 в досліджуваному трикутнику.
Побудуємо 3D рисунок функції двох змінних в Maple:
plot3d(x^2-x*y+y^2-4*x, y = 0 .. 4-2/3*x, x = 0 .. 6);

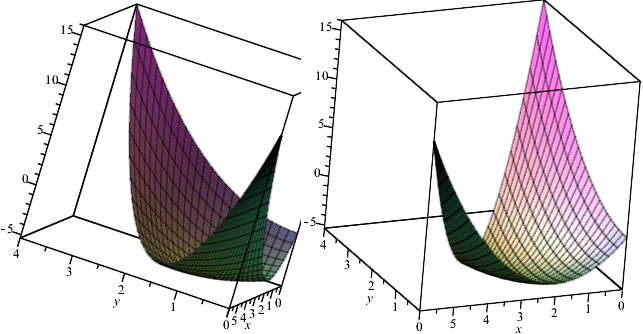
У Вас будуть інші функції двох змінних та області, які, як правило, не складні для побудови. Через похідні знаходите критичні точки в самій області, тоді як методом підстановки – на її границі. Далі в знайдених точках обчислюєте значення функції, та за результатами виписуєте де максимуми, а де мінімуми.