Умовний екстремум функції

Геометрична інтерпритація умовного екстремуму

Нехай поверхня S - графік функції z=f(x, y).
M1- точка безумовного екстремуму.
Нехай ℓ-крива, що описує рівняння зв'язку φ(x, y)=0.
L- відображення l на поверхню S.
M0- точка умовного екстремуму.

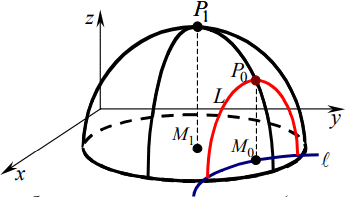
Задача полягає в знаходженні екстремуму z=f(x, y) за умови зв'язку φ(x, y)=0.

Метод виключення змінних (або метод підстановки)

З умови φ(x,y)=0 виразити y=ψ(x) [або x=ψ(y)] і підставити в функцію z=f(x, y).
Тоді умовний екстремум заданої функції = екстремум функції однієї змінної z=f(x, ψ(x)). [або z=f(y, ψ(y))].

Метод Лагранжа

Розглянемо лінії рівня f(x, y)=Ck.

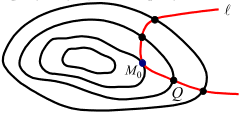
Точка умовного екстремуму M0 – це точка в якій ℓ дотикається до однієї з ліній рівня f(x,y)=Cm .
В точці умовного екстремуму дотична до лінії рівня
f(x,y)=Cm і ℓ – спільна.
Кутові коефіцієнти відповідно рівні

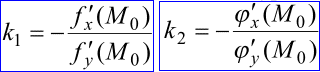
Якщо дотична спільна, то k1=k2, звідси виписуємо умову для знаходження точки екстремуму


Отримані з системи критичні точки M0 слід перевірити на умовний екстремум= встановити приріст Δf(M0) при умові зв'язку φ(x,y)=0.
Такий приріст рівний:

де F(x,y,λ)=f(x,y)+λφ(x,y) – функція Лагранжа (лагранжіан).

Алгоритм знаходження умовного екстремуму f(x,y)

І спосіб. Нехай задано функцію z=f(x,y) для якої потрібно знайти екстремуми при умові, що φ(x,y)=0 – рівняння зв'язку.
1) Задача умовного екстремуму зводиться до знаходження звичайного екстремуму функції Лагранжа
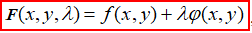(1)
λ - множник Лагранжа.
Спершу записуємо функцію F(x,y,λ).
2) Далі складаємо систему для визначення критичних точок.
Для цього обчислюємо часткові похідні лагранжіана, прирівнюємо їх до нуля.
3 рівняння системи це умова зв'язку
(2)
3) Характер умовного екстремуму можна встановити за знаком диференціала другого порядку функції Лагранжа:
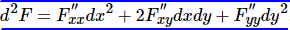(3)
Якщо у стаціонарній (критичній) точці d²F>0, то це є точка умовного мінімуму
(якщо у стаціонарній точці d²F<0, то це є точка умовного максимуму).
На практиці Лагранжіан часто позначають великою латинською L(x,y,λ).

2 спосіб. 3) Довести додатність квадратичної форми, або від'ємність іноді не просто через коефіцієнти при мішаних похідних.
Це Ви отримаєте на практичних, якщо функція та умова зв'язку підібрані так, щоб під диференціалом важко виділити повний квадрат.
Тоді застосовуйте другий спосіб визначення знаку диференціалу другого порядку функції Лагранжа:
З рівняння зв'язку маємо:

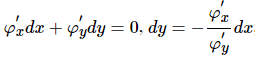
тому в кожній стаціонарній точці виконується
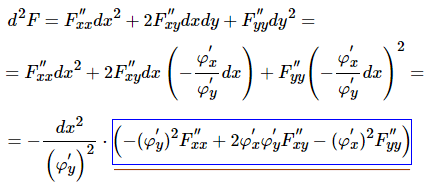(4)
Другий множник в квадратичній формі можна подати в такій формі
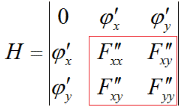(5)
Якщо H>0 то d²F<0, то маємо умовний максимум.
Якщо H<0 то d²F>0, і маємо умовний мінімум.
Часто ним користуються для зручності "гри" знаків,
H>0, +, максимум
H<0,-, умовний мінімум.
Якщо важко обчислювати визначник, можете виписувати лише дужку з (4) формули
H=-(φ'_y)²•F''_xx+2φ'_x•φ'_y•F''_xy-(φ'_x)²•F''_yy .
Покажемо як користуватися наведеними формулами для знаходження умовного екстремуму.

Приклади на умовний екстремум

Приклад 2.1 Знайти екстремум функції z=x²-y+3, за умови y-2x+5=0.
Розв'язання: 1 спосіб. Дане завдання можна зробити і через безумовний екстремум.
Для цього з умови зв'язку виразити змінну y(x):
y=2x-5
та підставити у функцію
z=x²-(2x-5)+3. (6)
Далі її дослідимо на екстремум
z'=2x-2.
З умови z'=0 дістанемо
2x-2=0,
x=1.
y(1)=2*1-5=-3.
M(1,-3) критична точка, значення в ній
z(1;-3)=1²-(2*1-5)+3=7.
Щоб перевірити чи локальний максимум чи мінімум досягається підставимо в (6) будь-яку точку рядом, зокрема в нулі дістанемо
z(0)=0-0+5+3=8.
Значення більше ніж в критичні точці, отже в останній досягається локальний мінімум.
Ось так швидко, без складних формул та обчислень встанвили критичну точку (1;-3) та з'ясували, що в ній маємо локальний мінімум.
Локальний, тому що за умови y-2x+5=0.
Глобальний екстремум функції двох змінних z=x²-y+3 інший і його шукають на всій множині визначення, а не тільки на кривій.
Тепер перегляньте та порівняйте з методом Лагранжа.

2 спосіб. 1) Складаємо лагранжіан
L(x,y,λ)=x²-y+3+λ(y-2x+5).
2) Знайдемо часткові похідні L:

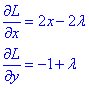
Виписуємо та розв'язуємо систему рівнянь:

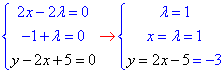
тоді z=1^2-(-3)+3=7.
(1;-3) - стаціонарна точка.
Знайдемо часткові похідні ІІ порядку функції L(x,y,λ) в стаціонарній точці та підставимо в формулу диференціалу

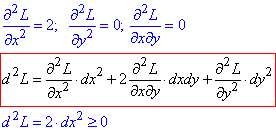
Оскільки d²L≥0, то точка (1;-3) є точкою умовного мінімуму функції z=x²-y+3, тобто
z_min=7.

Перший спосіб швидший, але щоб це відчути треба самостійно очислити хоча б з десяток прикладів першим та другим методом.
Для візуалізації поверхні z та площини з умови зв'язку наведемо фрагмент коду, як побудувати тримірні графіки в пакеті Maple
with(plots):
q1 := plot3d(x^2-y+3, x = -4 .. 4, y = -8 .. 4):
q2:=implicitplot3d(y-2*x + 5=0, x = -7 .. 5, y = -8 .. 5, z = 0 .. 20):
plots[display](q1, q2);

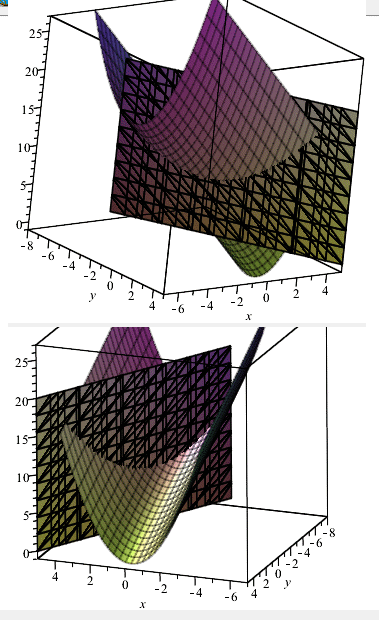
Приклад 2.2 Дослідити на умовний екстремум z=x+3y, якщо x²+y²=10.
Розв'язання: Складаємо функцію Лагранжа та знаходимо її часткові похідні за змінними "ікс" та "ігрик":

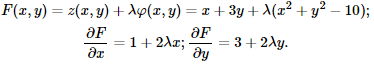
Прирівняємо похідні до нуля, добавимо до них умову зв'язку та з отриманої системи рівнянь знайдемо стаціонарну точку та множник Лагранжа λ:

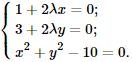
Якщо припустити, що λ=0, то перше рівняння перетвориться на 1=0. З цього слідує, що λ≠0 і на нього можна ділити.
Тепер маємо право з перших двох рівнянь виразити "ікс, ігрик":

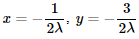
та підставити в рівняння зв'язку (3).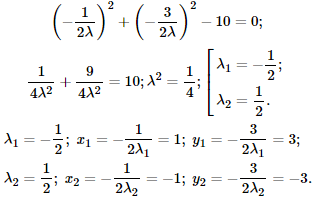

Після розрахунків бачимо, що система має два розв'язки, отже є дві стаціонарні точки на контурі φ(x,y)=0.

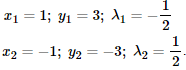
Зясуємо характер екстремума в точках М1(1;3) та M2(-1;-3).
Для цього побудуємо визначник

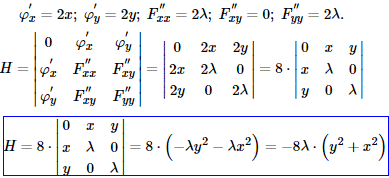
Обчислюємо значення в стаціонарних точках

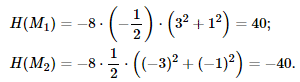
В точці М1(1;3) визначник H(M1)=40>0, тому в цій точці функція має умовний максимум
z_max(1;3)=1+3•3=10.
В точці M2(-1;-3) відповідний визначник H(M2)=-40<0 від'ємний, тому в цій точці функція двох змінних досягає умовного мінімуму
z_min(-1;-3)=-1+3•(-3)=-10.
Побудуємо тримірні графіки перетину площини та умови зв'язку (циліндра).
Для цього в Мейплі необхідно виконати фрагмент коду
q1 := plot3d(x+3*y, x = -4 .. 4, y = -4 .. 4);
q2 := implicitplot3d(x^2+y^2 = 10, x = -sqrt(10) .. sqrt(10), y = -sqrt(10) .. sqrt(10), z = -12 .. 12);
plots[display](q1, q2);
Отримаємо просторовий графік, який в пакеті Мейпл можна крутити вздовж 3 осей, нижче наведено фрагмент анімації з певних положень

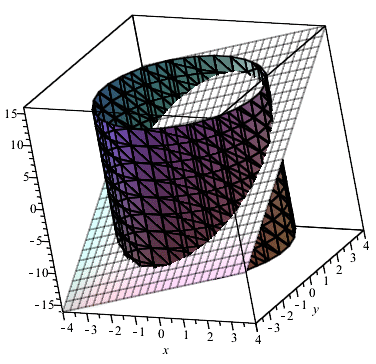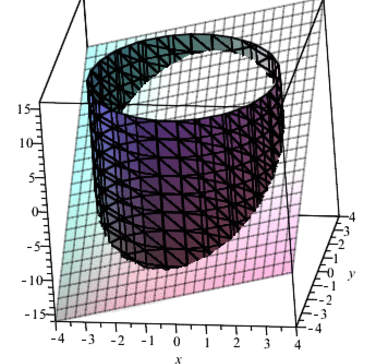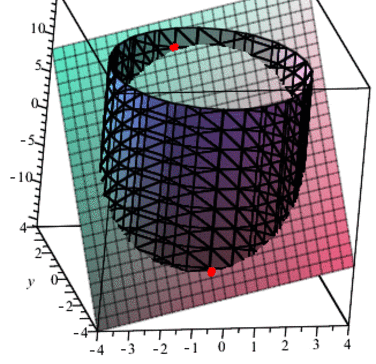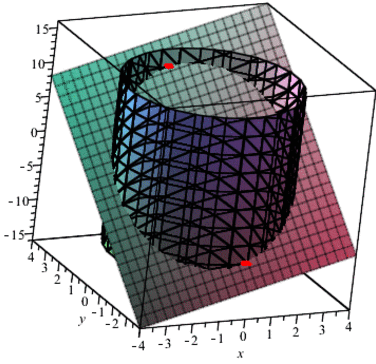
Приклад 2.3Визначити точки та характер екстремума функції
z=4-x²+2x-y²+4y
при рівнянні зв'язку y-x=0.
Розв'язання:Виділимо в рівнянні поверхні z(x,y) повні квадрати x та у
z=4-x²+2x-y²+4y=4-(x-1)²+1-(y-2)²+4=9-(x-1)²-(y-2)²
Отримане рівняння є параболоїдом обертання з вершиною в точці (1;2;9).
Те що перед змінними в квадратах в функції z стоять мінуси означає, що в точці (1;2) досягається максимум, також будь-яка точка локального екстремуму буде точкою максимуму.
Рівняння зв'язку y=x описує площину, а в площині Oxy пряму, тому доцільно розв'язати першим методом.
I. Підставимо рівняння зв'язку в функцію z(x,y)
z(x,y)=9-(x-1)²-(x-2)²
та дослідимо її на екстремум
z'=-2(x-1)-2(x-2)=-2x+2-2x+4=6-4x
z'=0 -> 6-4x=0
x0=6/4=1,5.
З умови зв'язку y=x дістанемо y0=x0=1,5.
Обчислимо значення функції в точці:
z(x0,y0)=9-(1,5-1)²-(1,5-2)²=8,5.
Припустимо, що ми не аналізували, що за поверхню нам задано.
І в нас немає часу, чи ми не хочемо його витрачати на пошук приросту функції за умови зв'язку.
Простим способом встановлення характеру локального екстремуму є підставлення точки з умови зв'язку, яка розміщена рядом і в якій легко знайти значення функції.
Для прикладу при умові y=x виберемо точку A(1;1) та знайдемо в ній значення
z(A)=9-(1-1)²-(1-2)²=8.
Порівнянням значень в точці умовного екстремуму та рядом
8,5>8
встановлюємо, що в точці M(1,5;1,5) функція z досягає максимуму z_max=8,5 за умови y=x.

II. Записуємо функцію Лагранжа
F(x,y,λ)=9-(x-1)²-(y-2)²+λ(y-x)
Обчислюємо часткові похідні І порядку F(x,y,λ):
F'_x=-2(x-1)-λ=-2x+2-λ;
F'_y=-2(y-2)+λ=-2y+4+λ.
Якщо продиференціювати F за множником Лагранжа λ та прирівняти до 0, то дістанемо умову зв'язку.
Тому система рівнянь для визначення критичних точок лагранжіана, це не що інше як рівність 0 диференціалу Лагранжа першого порядку.
Випишемо та розв'яжемо її
{F'_x=0,F'_y=0,F'_λ=0}
-2x+2-λ=0;
-2y+4+λ=0;
y-x=0.
Зтретього рівняння виразимо y=x та підставимо в друге
-2x+2-λ=0;
-2x+4+λ=0.
Віднімемо від другого рівняння перше
2+2λ=0 -> λ=-1.
Далі визначаємо критичну точку
2x=2-λ=3 -> x0=1,5;
2y=4+λ=3 -> y0=1,5.
Якщо функція складна, а умова зв'язку проста то y0 простіше виразити з умови, а не функції.
Щоб з'ясувати характер екстремуму, знайдемо другі похідні Лагранжіана
F''xx=(-2x+2-λ)'x=-2
F''xy=(-2x+2-λ)'y=0
F''yy=(-2y+4+λ)'y=-2.
Тоді диференціал другого порядку в точці (x0;y0)
d²F=-2dx²-2dy²<0
є від'ємним, тому робимо висновок, що функція досягає умовного максимума
z_max(x0,y0)=8,5
Побудуємо графік функції в мейплі
plot3d(9-(x-1)^2-(y-2)^2, x = -1 .. 3, y = 0 .. 4, axes = normal);

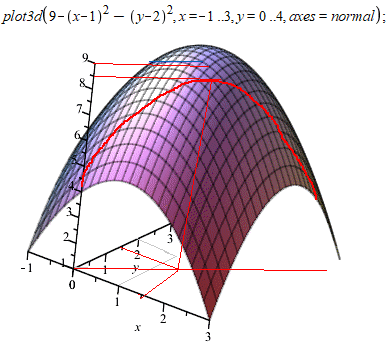
Вважаємо, що умовні екстремуми Ви після цього уроку знайти зможете, залишилося пояснити як будувати дотичну та нормаль до поверхні та ще кілька тем, пов'язаних з функціями багатьох змінних.