Задача 8 Досить довга нитка рівномірно заряджена з лінійною густиною 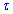 .
.
Визначити модуль E напруженості електричного поля в точці A, яка міститься навпроти кінця нитки на відстані a від неї.
Дано: | Розв’язання: |
Знайти: |
Відповідь: 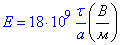
Задача 10 Однакові точкові заряди q1=q2=3 нКл розміщені на відстані l=10 см один від одного.
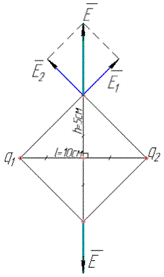
Визначити напруженість E електричного поля у точках, які лежать на перпендикулярі до середини відрізка, що сполучає заряди на відстані h=5 см від середини.
Дано: |
| Розв’язання: |
Знайти: |
Модулі векторів напруженості електричних полів, створених І і ІІ зарядом:
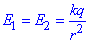 , де q=q1=q2.
, де q=q1=q2.
Модуль вектора напруженості результуючого електричного поля визначимо за теоремою Піфагора:
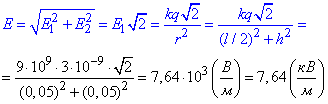 .
.
(Якщо проектувати напруженості на вісь, то 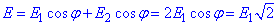 ).
).
Відповідь: 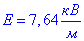
Задача 11 Тонке кільце, радіус R=10 см, рівномірно заряджене з лінійною густиною 8 нКл/м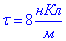 .
.
Визначити модуль E напруженості електричного поля у точках, що лежать:
а) на осі кільця на відстані x=15 см від його центра;
б) у центрі кільця;
в) на великій відстані x>>R від кільця.
Дано: 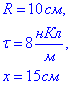 |
| Розв’язання: |
Знайти: |
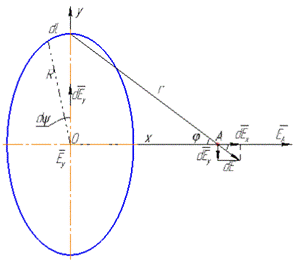
Розіб'ємо кільце на множину елементів dl, заряд кожного з яких 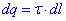 можна вважати точковим.
можна вважати точковим.
Довільний із цих елементів створює у точці A поле елементарної напруженості 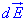 , вектор якої розкладемо на дві компоненти, відповідно, вздовж осі кільця
, вектор якої розкладемо на дві компоненти, відповідно, вздовж осі кільця 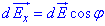 та перпендикулярно до неї
та перпендикулярно до неї 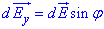 .
.
Величину вектора 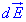 шукають за формулою:
шукають за формулою: 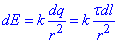 , де r - відстань від елементарного заряду до точки A.
, де r - відстань від елементарного заряду до точки A.
З рисунка видно, що 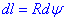 ,
, 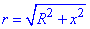 , а
, а 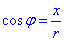 і
і 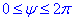 (вздовж кільця). Отже,
(вздовж кільця). Отже,
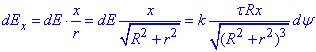 .
.
Щоб відшукати підсумкову напруженість EA поля в точці A досить проінтегрувати наведений вище вираз dEx по всій довжині кільця
(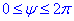 ), оскільки інтеграл по контуру рівний нулю
), оскільки інтеграл по контуру рівний нулю 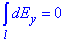
(для кожного елемента кільця dl знайдеться симетричний до нього відносно центра O з протилежною складовою елемента напруженості -dEy, які у разі додавання взаємно компенсуються).
Отож, підсумковий вектор 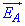 спрямований вздовж осі кільця, а його величина
спрямований вздовж осі кільця, а його величина
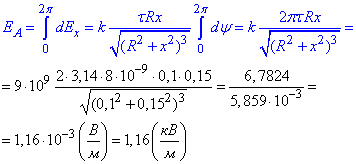
б) Оскільки інтеграл по контуру від електричної напруженості рівний нулю 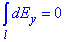 , то модуль напруженості електричного поля в центрі кільця (в точці O):
, то модуль напруженості електричного поля в центрі кільця (в точці O):
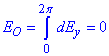
в) модуль напруженості електричного поля на великій відстані x>>R від кільця (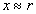 )
)
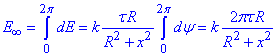 .
.
Відповідь: 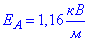
Задача 12 Вважаючи протон і електрон, з яких складається атом водню, за точкові заряди, що розміщуються на відстані 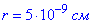 , визначити модуль напруженості E електричного поля в точках B і C (рис.).
, визначити модуль напруженості E електричного поля в точках B і C (рис.).
Дано: |
| Розв’язання: |
Знайти: |
Вектор напруженості результуючого електричного поля знайдемо за принципом суперпозиції полів: 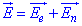 .
.
Модуль напруженості 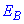 електричного поля в точці B (проекція векторів
електричного поля в точці B (проекція векторів 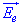 і
і 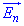 в точці B на вісь x, бо
в точці B на вісь x, бо 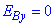 ):
):
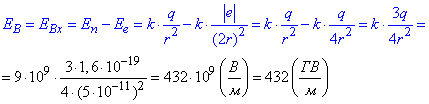
Спроектуємо модуль напруженості EC електричного поля в точці C на осі:
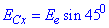 - проекція на вісь x;
- проекція на вісь x;
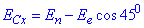 - проекція на вісь y.
- проекція на вісь y.
Тоді
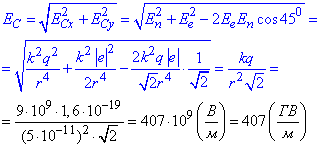
Відповідь: 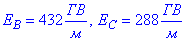
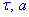
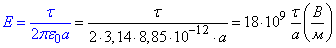 ,
,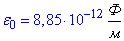 - електрична стала
- електрична стала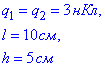
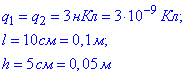
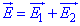 .
.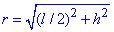 .
.
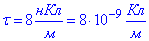 - лінійна густина заряду.
- лінійна густина заряду.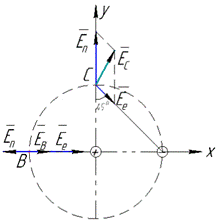
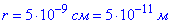 .
.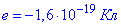 ,
,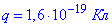 .
.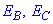 ,
, 
