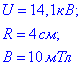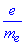Визначити відношення заряду електрона до його маси при магнітній індукції B=10 мТл.

Задача 23 Електрон під дією електростатичного поля з різницею потенціалів U=14,1 кВ влітає в однорідне магнітне поле перпендикулярно до ліній його індукції і рухається по колу радіусом R=4 см.
Визначити відношення заряду електрона до його маси, якщо магнітна індукція B=10  мТл.

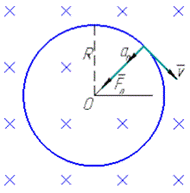
 Рух зарядженої частинки в однорідному магнітному полі         буде відбуватись по колу (див. рисунок), якщо частинка влетить в магнітне поле перпендикулярно до ліній магнітної індукції, тобто .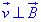
Оскільки сила Лоренца перпендикулярна до вектора 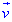, то вона надасть частинці (електрону) нормального прискорення a_n.
Згідно з ІІ законом Ньютона:

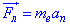
На рисунку траєкторія електрона суміщена з площиною креслення і вказаний (довільно) напрям вектора .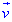
Силу Лоренца спрямовуємо перпендикулярно до вектора 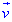до центра кола.
Модуль сили Лоренца: 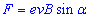, у нашому випадку 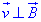і 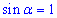, тоді
.
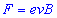Модуль нормального прискорення:
.
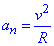Отже,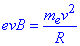
Звідси маємо

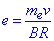
Зазначимо, що 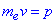- імпульс електрона, тому .  (*)
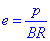Імпульс електрона знайдемо, скориставшись зв'язком між роботою сил електричного поля і зміною кінетичної енергії електрона, тобт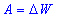о , або
,
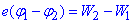де 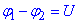- різниця потенціалів (спад напруги);
W₁, W₂ - початкова і кінцева кінетична енергія електрона.
Нехтуючи початковою кінетичною енергією електрона 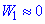і виразивши кінетичну енергію W₂ через імпульс p
(а саме 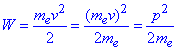), отримаємо
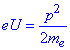, звідси 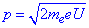і підставимо у формулу (*):

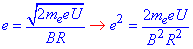
отже обчислимо заряду електрона до його маси:
.

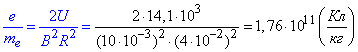Відповідь: 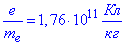.