Дослідження функції не обходиться без встановлення інтервалів опуклості та вгнутості, причому їх можуть розділяти як точки перегину, так і критичні точки ІІ роду. Все залежить від ряду правил, які Вам прийдеться запам'ятати із наведеного теоретичного матеріалу.
Крива y=f(x) називається опуклою на інтервалі 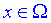 , якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
Крива y=f(x) називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої.
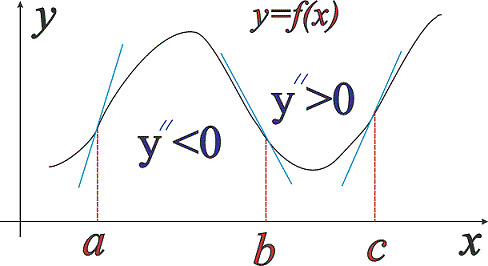
На рисунку вище крива опукла на інтервалі (a;b) та вгнута на (b;c), в точці x=b - функція має перегин.
Опуклість і вгнутість кривої, яка є графіком функції y=f(x) характеризується знаком її другої похідної: якщо в деякому інтервалі друга похідна менша нуля f''(x)<0 то крива опукла на цьому інтервалі , а якщо більша f''(x)>0 то крива вгнута на цьому інтервалі.
Інтервали опуклості і вгнутості можуть відділятися один від одного або точками, де друга похідна дорівнює нулю, або точками, де друга похідна не існує. Ці точки називаються критичними точками II роду.
Якщо при переході через критичну точку II роду друга похідна f''(x) змінює знак, то графік функції має точку перегину(x0, f(x0).
Схема знаходження точо перегину графіка фунції
1) знайти область визначення функції;
2) знайти критичні точки II роду xi функції y=f(x);
3) дослідити знак другої похідної y=f''(x) в інтервалах, на які критичні точки ділять область визначення функції D(f). Якщо критична точка x0 поділяє інтервали, де друга похідна f''(x) справа і зліва має різні знаки, то x0 є абсцисою точки перегину графіка функції;
4) обчислити значення функції (ординати) y(x0) в точках перегину.
Приклади. Знайти точки перегину і інтервали опуклості та вгнутості графіків функцій. (Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )
І) (5.827) y=x4-4x3-18x2+2x-1
Розв'язування: 1) Область визначення полінома вся дійсна множина 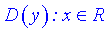
2) Знаходимо критичні точки функції ІІ роду
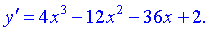
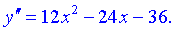
Прирівнюємо другу похідну до нуля
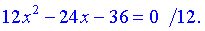
x2-2x-3=0.
Квадратне рівняння матиме наступні корені
x=-1; x=3.
Вони розбивають область визначення на 3 інтервали опуклості або вгнутості
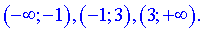
3) Визначаємо знак похідної підстановкою значень з інтервалів
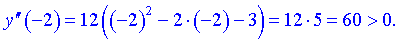
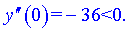
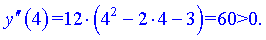
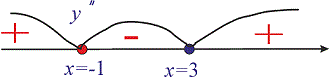 З аналізу знаків слідує, що функція вгнута на інтервалах
З аналізу знаків слідує, що функція вгнута на інтервалах 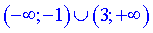 та опукла при
та опукла при 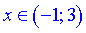 . Точки x=-1; x=3 є точками перегину, оскільки друга похідна в них змінює знак.
. Точки x=-1; x=3 є точками перегину, оскільки друга похідна в них змінює знак.
4) Обчислюємо значення функції
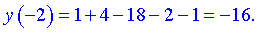
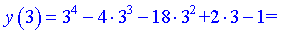
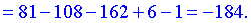
A(-1; -16), B(3; -184) – точки прегину.
Щоб матеріал Вам добре запам'яттався, до цього завдання і наступних наведу графіки функцій із знайденими критичними точкамию. Це допоможе уявити, як точки перегину виглядають на реальних графіках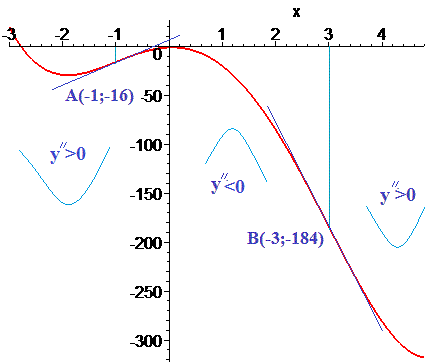
ІІ) (5.831) y=2x3-x4+36x2-100
Розв'язування: 1) Область визначення - множина дійсних чисел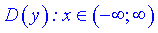 .
.
2) Критичні точки II роду: знайдемо другу похідну функції
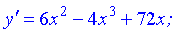
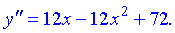
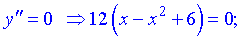
-x2+x+6=0.
Розв'яжемо квадратне рівняння
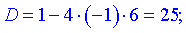
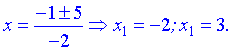
Друга похідна y'' існує на всій області визначення.
3) Визначаємо знаки другої похідної y'' на проміжках, де друга похідна відмінна від нуля
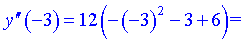
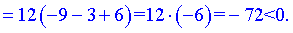
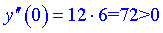
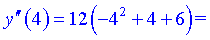
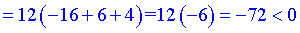
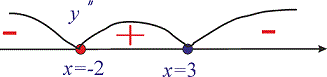 Таким чином, отримаємо два інтервали опуклості
Таким чином, отримаємо два інтервали опуклості  та один вгнутості графіка функції (-2;3).
та один вгнутості графіка функції (-2;3).
4) Знайдемо значення функції в точках перегину
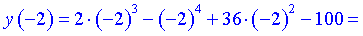
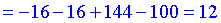
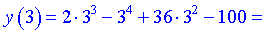
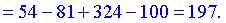
A(-2; 12), B(3; 197) -точки перегину функції. Частина графіку з проаналізованими точками перегину наведена нижче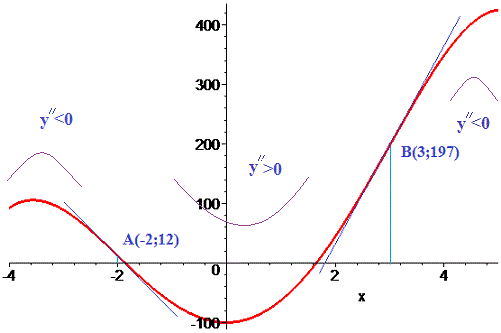
ІІІ) (5.834)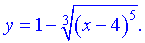
Розв'язування: 1) Область визначення є вся множина 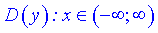 , так як корінь кубічний існує з від'ємних чисел.
, так як корінь кубічний існує з від'ємних чисел.
2) Критичні точки знайдемо з умови рівності нулю або неіснування другої похідної функції
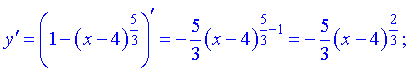
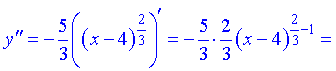
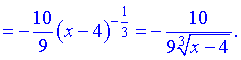
Друга похідна існує на всій області крім точки x=4.
3) Попередні дослідження показали, що точка x=4 розбиває область визначення на два інтервали 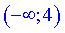 і
і 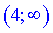 . Для встановлення, який з них буде інтервалом опуклості або вгнутості, підставимо точки справа і зліва від критичної в другу похідну.
. Для встановлення, який з них буде інтервалом опуклості або вгнутості, підставимо точки справа і зліва від критичної в другу похідну.
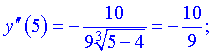
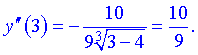
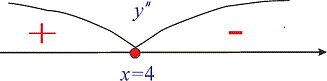 З цього слідує, що на інтервалі
З цього слідує, що на інтервалі 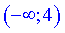 крива вгнута, а на
крива вгнута, а на 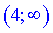 – опукла. Досліджувана точка x=4 є точкою перегину.
– опукла. Досліджувана точка x=4 є точкою перегину.
4) В точці перегину функція приймає значення
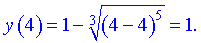
A(4; 1) – точка перегину. Графік функції наступний
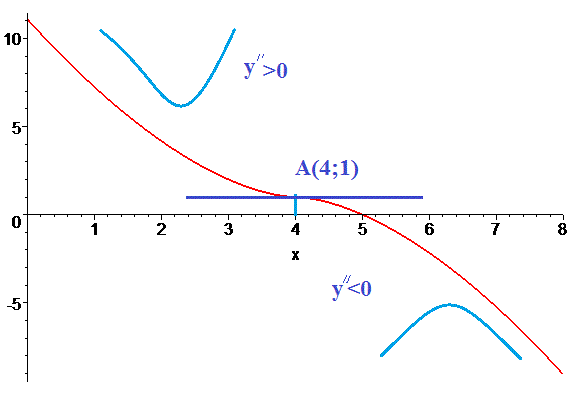
IV) (5.835)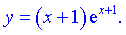
Розв'язування: 1) Область визначення 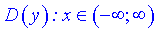 , оскільки експонента визначена на множині R.
, оскільки експонента визначена на множині R.
2) Встановлюємо критичні точки ІІ роду
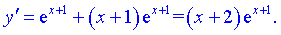
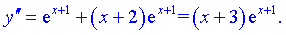
З умови рівності нулю другої похідної отримаємо
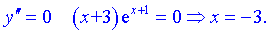
Знайдена точка розбиває область визначення на два інтервали 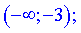
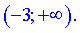
3) Дослідимо знаки на знайдених інтервалах
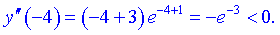
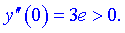
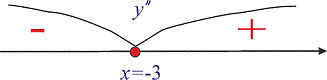
На першому інтервалі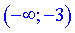 графік функції опуклий, а на
графік функції опуклий, а на 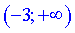 вгнутий. Точка x=-3 є абсцисою точки перегину.
вгнутий. Точка x=-3 є абсцисою точки перегину.
4) Знаходимо ординату
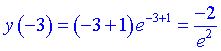
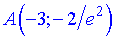 – точка перегину. Графік кривої має вигляд
– точка перегину. Графік кривої має вигляд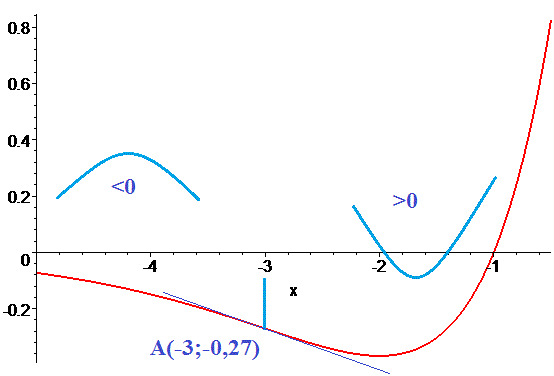
V) (5.845) 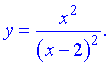
IV)1) Областю визначення є множина значень, при яки знаменник не перетворюється в нуль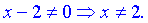
Отримуємо два інтервали визначеності дробової функції
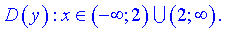
2) Для відшукання критичних точок диференціюємо функцію двічі
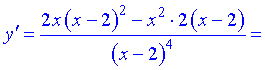
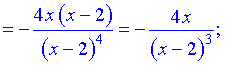
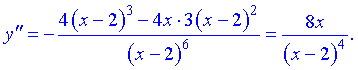
Друга похідна рівна нулю при x=0 і не існує в точці x=2.
3) Дослідимо знаки похідної на інтервалах 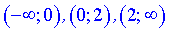 методом підстановки значень
методом підстановки значень
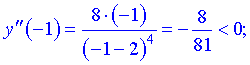
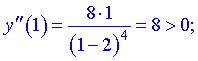
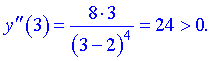
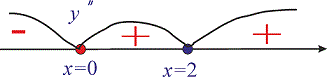 Отримали один інтервал де графік функції опуклий
Отримали один інтервал де графік функції опуклий 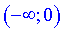 та два
та два 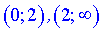 де він вгнутий.
де він вгнутий.
4) В точці перегину x=0 функція прийме значення y(0)=0, A(0; 0), а її графіки мають вигляд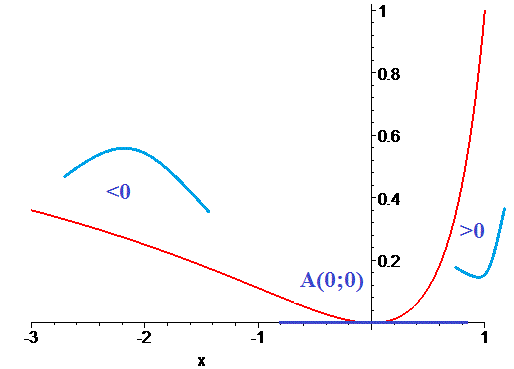
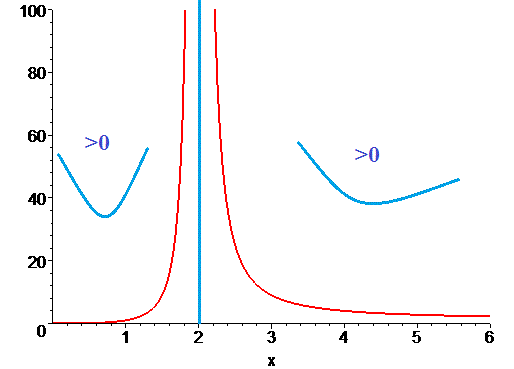
Правила знаходження точок перегину досить прості, потрібно лише добре вміти знаходити похідну. При знаходженні інтервалів досить важко привикнути, що функція опукла там де друга похідна від'ємна, і вгнута - при додатній другій похідній. Для цього потрібно розв'язати чимало задач і побудувати не менше графіків. Вчіться на наведених прикладах, розв'язуйте самостійно - це пришвидшить засвоєння теоретичного матеріалу.


