Під похідною вищих порядків розуміють диференціювання функції більше ніж один раз. Якщо похідну y'(x) повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції y=f(x), і вона позначається
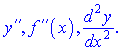
Похідна третього порядку матиме запис
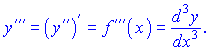
Аналагічно отримують формули для знаходження похідних вищих порядків. При знаходженні похідної (n+1) порядку необхідно знати похідну n-го порядку. Вийняток становлять функції, для яких можна помітити закономірність зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:
![]()
В інших випадках, для знаходження похідних вищих порядків від заданої функції потрібно послідовно знаходити всі її похідні нижчих порядків. Для практичного вивчення матеріалу розглянемо приклади.
Приклад 1. Обчислити похідні другого порядку
1) 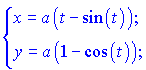
Розв'язок. За правилами диференціювання параметричних функцій маємо
![]()
Застосуємо до заданої функції. Знайдемо похідну y'
![]()
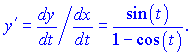
Диференціюємо функцію повторно. За правилом диференціювання отримаємо
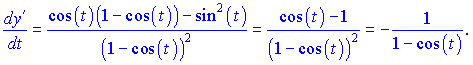
За формулою обчисюємо y''
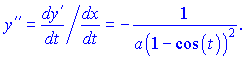
Вивчайте формулу другої похідної, вона не така очевидна для параметричної функції, але іншої немає.
2)![]()
Розв'язок. Визначаємо першу похідну для кореневої функції
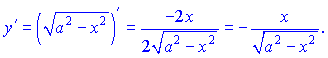
Обчислюємо другу похідну за правилом похідної частки
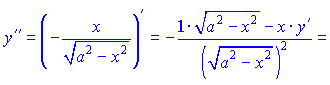
Ящо пи обчисленні Ви отримаи вираз другої похідної через першу, то потрібно замість першої підставити її значення. Добре перегляньте як тут спростиася підстанова першої похідної.
3)![]()
Розв'язок. Обчислимо першу похідну поліному
![]()
а потім другу
![]()
При знаходженні похідної другого і вищих порядків для даного прикладу і йому подібних можна користуватися наступним правилами:
(1) якщо степінь функції менший порядку похідної k, то даний доданок вкладу не дає
![]()
(2) всі старші степені дають вклад
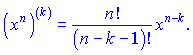
За такою схемою другу похідну можна було знайти за один прохід
![]()
![]()
Для практики другий спосіб ефективніший, особливо якщо потрібно знайти похідні набагато вищих порядків ніж другий.
4)y=e3x
Розв'язок. Похідна функції першого порядку матиме вигляд
![]()
Повторне диференціювання експоненти множником винесе степінь
![]()
По аналогії можна вивести формулу похідної експоненціальної функції k-го порядку
![]()
Розв'язуючи приклади для синус і косинус функцій можна замітити подібність при обчисленні старших похідних і вивести наступні залежності
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Користуйтеся формулами і нехай не виникає проблем з похідними вищих порядків.


