Щоб добре навчитися знаходити похідну Ви повинні не стільки знати на пам'ять, скільки вміти застосовувати на практиці таблицю похідних.

В першу чергу Вам необхідно запам'ятати правила виділені червоними рамками - правило суми, похідна добутку та частки функцій, як брати похідну складеної функції.
Далі йдуть розв'язки завдань на похідні погруповані в блоки по 10 прикладів, не найпростіші з тих, що Вам доводилося бачити онлайн. Проте, на нашу думку, вони навчать Вас швидко користуватися таблицею похідних та будуть добрим довідником при розв'язуванні практичних в 11 класах та далі у ВУЗ-ах. Кому важко їх розбирати почніть з попередніх уроків, там дещо простіші приклади.
Приклад 1. В усіх завданнях необхідно знайти перші похідні. Пояснень не потрібно, все містять формули, дано мінімальний опис перед кожним блоком які правила застосовували. Перший блок прикладів на перші 8 формул таблиці похідних.
Завдання 1,2 на правило похідної суми (3), 3 завд. на формулу (24), 4 - на похідну добутку функцій, 5, 6, 8, 9, 10 - похідну складеної функції, 7- похідна степневої функції (8) коли степені від'ємні.
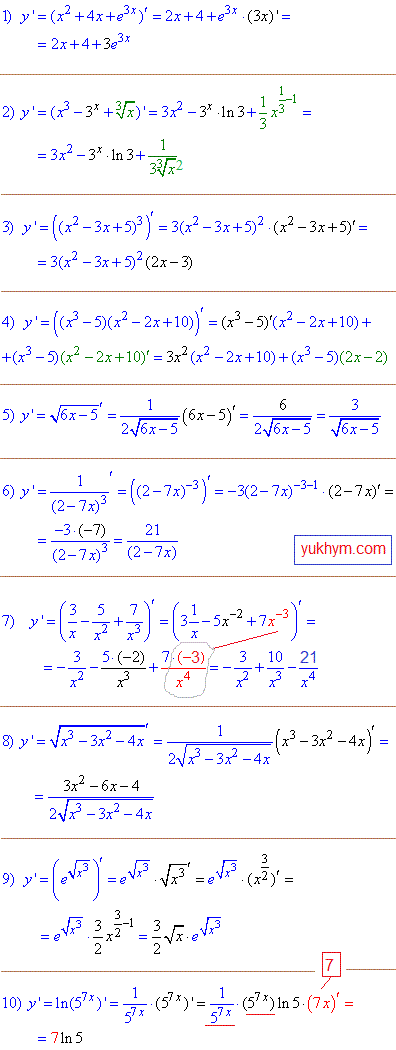
Приклад 2. В цьому блоці обчислюємо похідні на формули (10-13). Це експоненти, показникові функції та логарифми. Оскільки простіші приклади розібрані на попередніх уроках, то тут вчимося обчислювати похідні складених функцій. І щоб максимально наблизити до реалій практичних в багатьох завданнях вложеною функцією вибрано корінь квадратний, саме з ним в багатьох виникають труднощі на практичних та екзаменах.
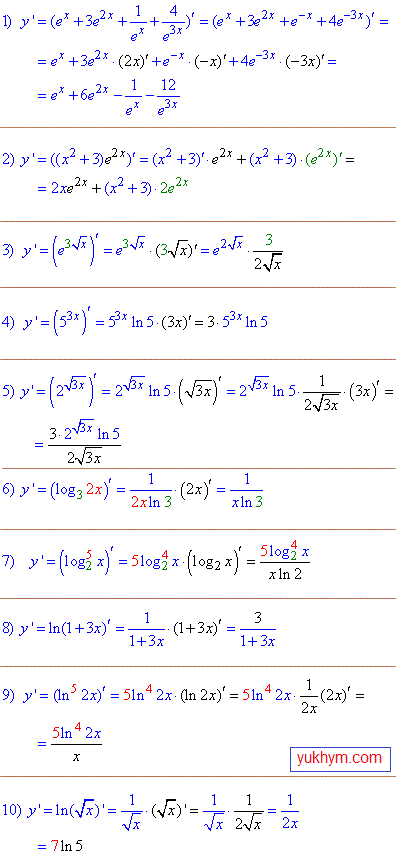
Приклад 3. Далі навчимося обчислювати похідні від тригонометричних функцій. Причому, аргументами в косинусах, синусах, тангенсах, котангенсах виступають складені функції. В більшості випадків лінійні (k·x), оскільки з ними найчастіше будете мати справу на практиці. Уважно розбирайте і запам'ятовуйте методику обчислення похідних.

Приклад 4. Окремої уваги заслуговують похідні обернених тригонометричних функцій. На екзаменах та практичних Ви повинні знати, як з допомогою формул (20-23) таблиці похідних обчислити аналогічні по складності завдання на арксинуси, арккосинуси. 7-10 завдання на похідні від арктангенса та арккотангенса, всюди складені похідні.
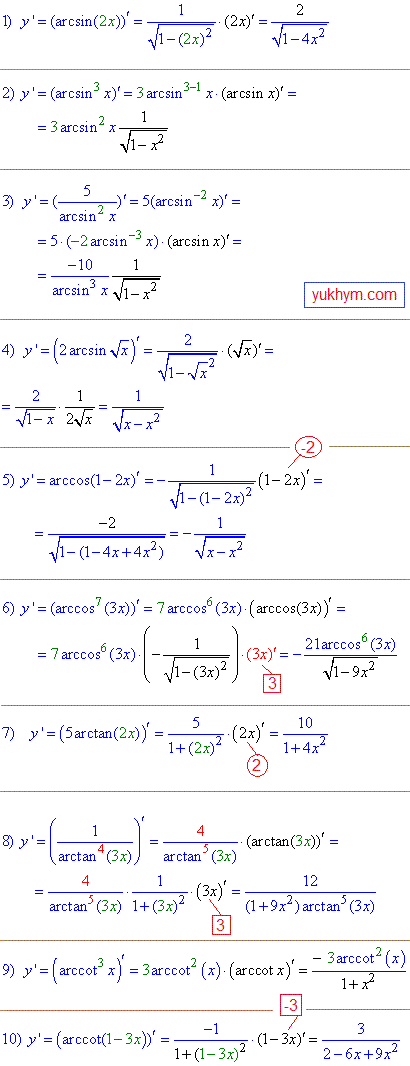
Приклад 5. В цьому блоці відібрано 10 готових відповідей на похідні добутку функцій. Поєднання добутків від коренів з синусами і експонент з логарифмами до степеневих та тригонометричних функцій.
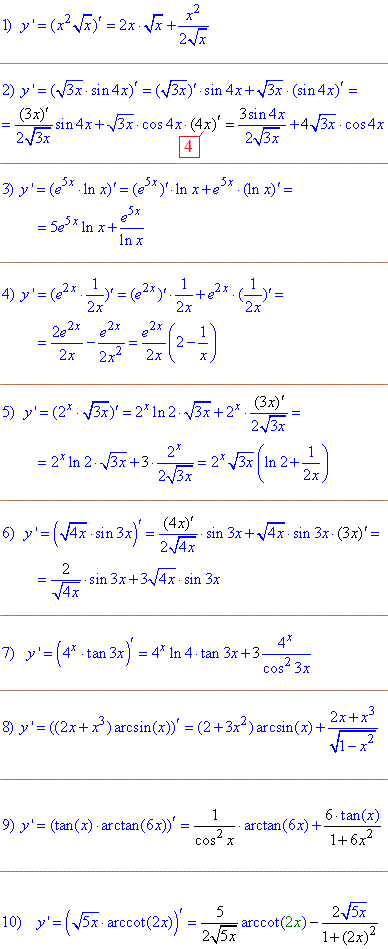
Пояснювати тут, що і для чого робили не будемо, все в наступній статті.
Окремо слід показати Вам чому рівні похідні гіперболічних та обернених гіперболічних функцій, але їх трохи багато, тому ми їх вирішили об'єднати та опублікувати новим уроком. Перед цим ще проаналізуємо з 20 прикладів на похідну добутку та частки функцій.


