Диференціал. Приклади наближених обчислень

Поняття диференціала взаємозв'язане з поняттям похідної, і е одним з фундаментальних в математиці. Сам термін "диференціал" (від латинського слова differentia – різниця) введений у математику Лейбніцом. Розглянемо виведення формули диференціалу.

Нехай маємо неперервну гладку функцію y=f(x) на проміжку [a;b]. Тоді вона має похідну на ньому і вона виражається залежністю

Відношення приросту функції до відношення приросту аргументу рівне

або

де похибка прямує до нуля якщо приріст аргументу прямує до нля , причому похибка обчислень - нескінченно мала величина порядку . Тому перший доданок

дає найбільший вклад та є головною частиною приросту функції, також він лінійний відносно приросту аргументу. Другий доданок при обчисленнях відкидають, а перший визначають при наближених обчисленнях та називають диференціалом функції

Диференціал незалежної змінної x рівний її приросту . Таким чином диференціал функції
dy=f'(x)dx
рівний її похідній, помноженій на диференціал незалежної змінної.
За рахунок простоти обчислень диференціал широко застосовується при дослідженні різноманітних процесів і явищ у фізиці, механіці, математиці. Будь-яка фізична величина протягом достатньо малого проміжку часу змінюється майже рівномірно, тому дійсний приріст величини, що характеризує її, можна замінити диференціалом цієї величини на даному проміжку часу. Таку заміну проводять доволі часто та називають лінеаризацією процесу.

ОСНОВНІ ВЛАСТИВОСТІ ДИФЕРЕНЦІАЛУ

Властивості диференціалу слідують із властивостей похідних.

1)

2)

3)

4)

5)

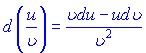
Розглянемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".

Приклад 1. (5.2.364) Який приріст матиме функція y=2x³-3x
при переході незалежної змінної від x₁=2 до x₁=2,01 ? Яке значення відповідної лінійної головної частини? Знайти відношення другої величини до першої.

Розв'язок. Обчислимо приріст функції за формулою




Визначимо значення лінійної головної частини функції. Для цього знайдемо похідну

та приріст аргументу

Підставимо в формулу диференціалу

Знайдемо відношення диференціалу до приросту аргументу

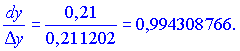
Отримали, що диференціал з точністю понад наближає приріст функції.

Приклад 2. (5.2.368) Дано функцію y=x⁵-4x.

При x=1 обчислити приріст і диференціал , даючи значення . Знайти відповідні значення відносної похибки

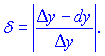
Розв'язок. Знайдемо значення функцій в точках




Далі обчислимо прирости функцій



Знайдемо похідну функції

та підставимо у формулу для визначення диференціалу



Обчислюємо відносні похибки



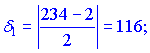
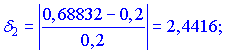
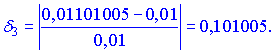
Задачу розв'язано. З неї слідує, що диференціал слід застосовувати при малих приростах аргументу, оскільки при великих – отримуємо велику похибку.

Приклад 3. Знайти диференціал функції

1) (5.2.380)

Розв'язок. Знайдемо похідну за правилом похідної добутку функцій

та підставимо у формулу диференціалу

Ось і всі розрахунки

2) (5.2.385)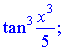

Розв'язок.Знаходимо похідну від тангенса, як від складеної функції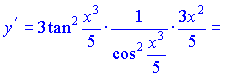

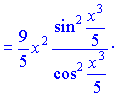
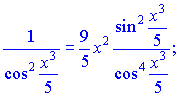
Обчислення непрості, спочатку беремо похідну від показника, далі від тангенса і вкінці від x³/5.
Записуємо диференціал функції

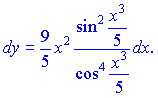
В знаменнику можна виділити квадрат косинуса і разом з чисельником записати як тангенс відповідного аргументу, а можна і залишити в такому вигляді.

3) (5.2.395)

Розв'язок. Диференціюємо арккосинус та підставляємо в формулу


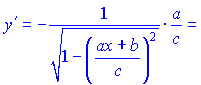
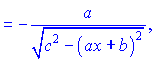
В результаті прийдемо до запису

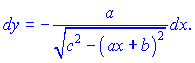
Основна суть диференціалу в наближених обчисленнях думаю Вам зрозуміла. Більше його прикладних застосувань Ви зрозумієте з наступних практичних заняттях.