Примеры пределов содержащие неопределенности вида ноль на ноль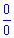 
часто встречаются в тригонометрических функциях. Для их раскрытия используют первый замечательный предел суть которого заключается в том, что предел отношения синус функции к аргументу, когда тот стремится к нулю равен единице
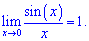
На основе этой формулы можно получить ряд полезных для практики пределов
1) 
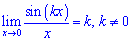
2) 
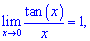
3) 
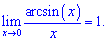
Второй замечательный предел позволяет раскрыть неопределенности вида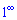 
.
Коротко он имеет следующую запись
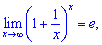
где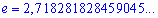 
–экспонента.
На основе второго замечательного предела получают следующие формулы
1) 
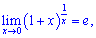
2) 
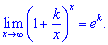
Примеры, которые сводятся к первому и второму замечательному пределу встречаются довольно редко, однако без них такие примеры не решить.
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. "Высшая математика" которые приводят к применению замечательных пределов.
-----------------------------------
Пример 1. Найти пределы функций.
1) (4. 388)
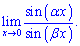
2) (4. 393)
3) (4. 399)
4) (4. 432)
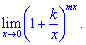
5) (4. 437)
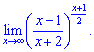
6) 
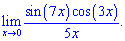
7) 
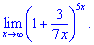
Решение.
1) Домножим числитель и знаменатель на аргумент и сведем к первой замечательной границы
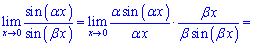
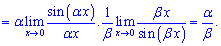
2) Разделим числитель и знаменатель на аргумент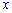
и сократим
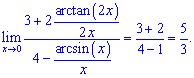
3) Согласно разложению корня в окрестности единицы
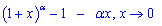
знаменатель возможно превратить следующим образом
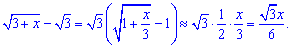
На основе этого и находим предел
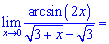
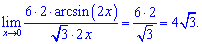
4) Сведем к второму замечательному пределу
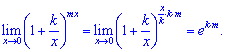
5) Сведем к правильной дроби выражение в скобках
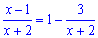
и подставим в предел
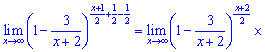
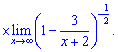
Вычислим первый множитель
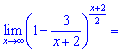
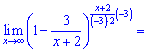
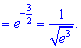
Второй предел равна единице
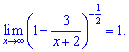
Окончательно получим
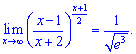
6) Сведем решение к первому замечательному пределу
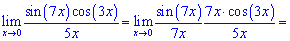
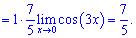
7) Преобразуем показатель для применения второго замечательного предела
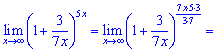
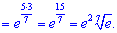
Подобных примеров можно привести много, они встречаются в контрольных, тестах, екзаменах. Их решения позволит закрепить Вам лучшие практические навыки поэтому пробуйте решать самостоятельно. Если в обучении вам встретятся тяжелые пределы посчитать которые Вы не в состоянии обращайтесь к нам. Мы Вам в этом поможем!
-----------------------------------
Посмотреть материалы:
