Уважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к экзаменам, тестам, внешнему независимому тестированию по математике в 2015 году. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике. Решение примеров будут интересны для школьников 9, 10, 11 классов, а так же их родителей.
Раздел II. Уравнения и неравенства
Задача 2.34 Решите уравнение с корнями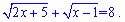 
Если уравнение имеет один корень, впишет его в ответ; если два корня - впишите их сумму.
Решение: Задано иррациональное уравнение, поэтому сначала исследуем область определения корней:
2x+5>0; x>-5/2=-2,5
x-1>0; x<1.
Общим для двух является интервал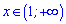 
, на нем и будем искать решение.
Возносим обе части уравнения к квадрату и упрощаем
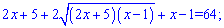
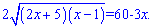
Опять получили уравнение с корнем, чтобы избавиться иррациональности подносим к квадрату
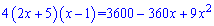
После группировки слагаемых получим квадратное уравнение
x2-372x+3620=0.
Вычисляем дискриминант
D=3722-4*3620=123904
и корни уравнения
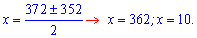
Оба корня принадлежат ОДЗ, следовательно по условию задачи находим их сумму
362+10=372.
Ответ: 372.
Задача 2.35 Решите уравнение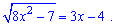 
Если уравнение имеет один корень, впишет его после слова "Ответ", если несколько корней, впишет их сумму.
Решение: Имеем уравнение с корнем, поэтому выписываем ОДЗ из условия ограничения на подкорнневую функцию
x2>7/8.
Далее подносим к квадрату обе части и сводим к квадратному уравнению
8x2-7=9x2-24x+16;
x2-24x+23=0
Поскольку коэффициенты отличаются на единицу, то решение находим по теореме Виета.
(x-23)(x-1)=0;
x=23; x=1.
Поскольку x = 1 не входит в ОДЗ, то x = 23 - единственное решение уравнения.
Ответ: 23.
Задача 2.36 Решите уравнение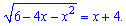 
Если уравнение имеет несколько корней, то в ответ запишите их сумму. Если уравнение имеет один корень, то запишите его в ответ.
Решение: Для данного уравнения ОДЗ находить не будем, а лишь проверим корни в конце вычислений подстановкой. Это порой помогает сохранить несколько минут на тестах. Подносим к квадрату, чтобы избавиться иррациональности
6-4x-x2=x2+8x+16;
2*x2+12*x+10=0;
x2+6*x+5=0.
Вычисляем дискриминант и корни уравнения
D=62-4*5=36-20=16
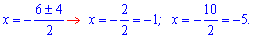
Выполним подстановку
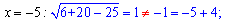
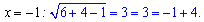
Один корень лишний, таким образом x=-1 – единственный корень иррационального уравнения.
Ответ: -1.
Оставайтесь с нами и подготовка к ВНО 2015 по математике останется для Вас приятным воспоминанием и сэкономит много времени и денег на репетиторов. Помощь по математике в виде готовых решений облегчит учебу всех школьников и будет хорошей инструкцией на экзаменах и тестах.
