Иррациональными называют уравнения в которых неизвестная величина находится под знаком корня определенного степени. Простейшие иррациональные уравнения решаются или подъемом в степень или заменой . Сложные иррациональные уравнения сводятся к предыдущим некоторыми искусственными методами . Например, такое на первый взгляд сложное уравнение
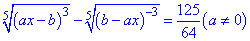
сводится к квадратному заменой
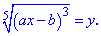
Зачастую при раскрытии иррациональности используют формулу сложного радикала
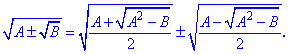
Стоит отметить, что при решении иррациональных уравнений необходимо определять область допустимых значений. Кроме того следует производить проверку, подставляя найденные значения неизвестных в исходное уравнение, поскольку при возведении в степень мы увеличиваем степень уравнения что может привести к появлению посторонних корней.
Перейдем к вычислениям.
Пример 1. Найти решение уравнения
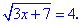
Решение:
Находим область допустимых значений
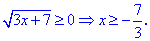
Подносим обе части уравнения в квадрат и решаем
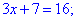
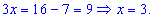
Получили решение x=3.
-------------------------
Пример 2. Найти решение уравнения
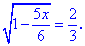
Решение:
ОДЗ для уравнения
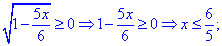
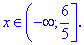
Раскрываем иррациональность уравнения и находим
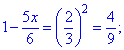
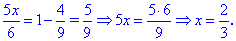
Он принадлежит области допустимых значений , то есть - является решением.
-------------------------
Пример 3. Решить уравнение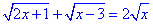
Решение:
Находим область допустимых значений
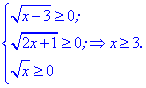
ОДЗ: 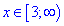
По описанной схеме подносим обе части в квадрат чтобы избавиться иррациональности
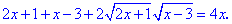
Переносим все слагаемые кроме корней в правую часть и упрощаем
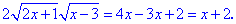
Для раскрытия иррациональности снова выполняем возведения в квадрат и упрощение
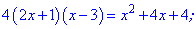
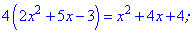
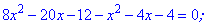
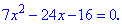
Получили квадратное уравнение, корни которого находим с помощью дискриминанта
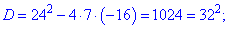
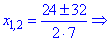
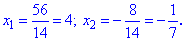
Второй корень не принадлежит области допустимых значений . Эту проверку следует выполнять всегда , иначе получите больше корней чем нужно, причем они не удовлетворяют исходное уравнение .
Итак решением будет значение x=4.
-------------------------
Пример 4. Решить уравнение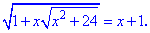
Решение:
Область допустимых значений для данного уравнения в простой способ найти не удастся , поэтому выполним решение после чего проверим подстановкой полученные корни.
Подносим обе части уравнения в квадрат
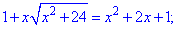
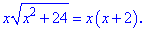
Данное выражение большинство из Вас упростило бы на x и подносило к квадрату. Но это было бы неправильно.
На x делить можно когда он принимает ненулевое значение. В данном случае x=0 будет решением уравнения , в чем легко убедится
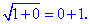
После того, как мы это учли можно продолжать вычисления
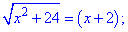
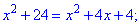
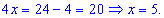
Выполняем проверку
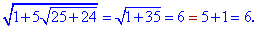
Получили два корня уравнения x=0, x=6.
-------------------------
Пример 5. Найти решение уравнения
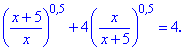
Решение:
Преподносить к квадрату обе стороны в подобных уравнениях не нужно. Для упрощения делаем замену
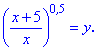
Уравнение превратится в следующее
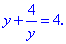
Умножаем на y и переписываем в виде квадратного уравнения
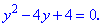
Теорема Виета дает нам два одинаковые корни
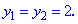
Возвращаемся к замене и находим решение
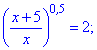
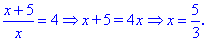
Значение x=5/3 удовлетворяет уравнения.
-------------------------
Пример 6. Найти решение иррационального уравнения
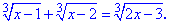
Решение:
Подносим к кубу обе стороны и упрощаем
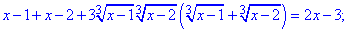
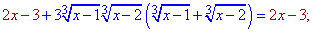
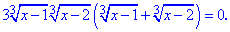
Стоит отметить, что выражение в скобках соответствует правой стороне заданного уравнения. В подобных примерах такие ситуации встречаются часто, поэтому будьте внимательны при решении . Делаем подстановку
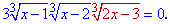
Приравниваем каждый из множителей к нулю и решаем
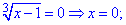
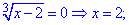
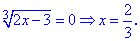
Проверку выполните самостоятельно. Она покажет что все три найденные значения превращают уравнения в тождество.
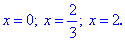
-------------------------
Пример 7. Найти решение иррационального уравнения
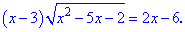
Решение:
Такой тип уравнений придуман для невнимательных студентов. При спокойном анализе можно увидеть следующую закономерность

Стандартное возведения в квадрат в данном случае было бы длинным и сложным путем к отысканию решений. С скобок получим значение
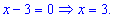
Упрощаем исходное уравнение и подносим к квадрату
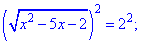
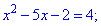
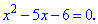
К полученному квадратного уравнения вычисляем дискриминант
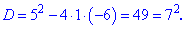
Корни уравнения находим по формуле
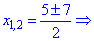
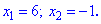
Таким образом установлено, что подобные уравнения могут иметь до трех решений
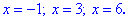
Изучайте по возможности различные математические пакеты - они облегчают обучение . В частности, в Maple последнее задача решается несколькими строками
> restart;
> eq:=(x-3)*sqrt(x^2-5*x-2)=2*x-6;
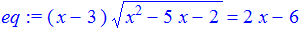
> solve({eq},{x});
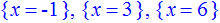
Просто и красиво . Однако и Maple может решить далеко не все иррациональные уравнения, некоторые корни не находит, в определенных случаях покоренных выражения нужно доопределить. Однако для упрощения расчетов достаточно проста в плане кода программа.
----------------------------
На этом знакомство с иррациональными уравнениями завершается . На практике можно встретить иррациональные уравнения которые вообще говоря трудно решить приведенными методами, однако приближенные корни найти численно удается. Поэтому, если у Вас при исчислении возникнут трудности - обращайтесь, мы Вам поможем!
Похожие материалы:


