Уважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к экзаменам, тестам, внешнему независимому тестированию по математике в 2015 году. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике. Решение примеров будут интересны для школьников 9, 10, 11 классов, а так же их родителей.
Раздел II. Уравнения и неравенства
Задача 2.32 (Т-06, 41) Задано 4 уравнения:
1. 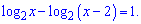
2. 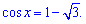
3.|x+2|=-3.
4. 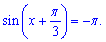
Укажите уравнение, которое не имеет корней на множестве действительных чисел.
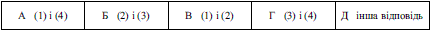
Решение:
1. Начнем анализ с логарифмического уравнения. Его можно переписать в виде
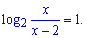
Область допустимых значений x>2. Решение логарифмического уравнения находим из условия
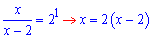
х=2*х-4;
2х-х=4; х=4.
Уравнение имеет один корень.
2. Оценим правую сторону уравнения, если она по модулю не превышает единицу то корень существует.

Итак косинус с таким значением не существует.
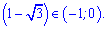
3. |x+2|=-3 – уравнение с модулем не имеет корней, поскольку модуль отрицательным быть не может.
4. По аналогии с косинусом, синус по модулю не должен превышать единицу.
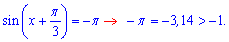
Однако Pi больше единицы, следовательно уравнение не имеет корней. Подытоживая написанное выше 3 и 4 уравнения не имеют корней.
Это соответствует варианту Г ответов к тестовым заданиям.
Ответ: Г.
В задачах 2.33 - 2.86 правильный ответ оценивается 2 баллами.
Задача 2.33 (Т-06, 26) Решите иррациональное уравнение
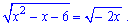
Если уравнение имеет один корень, запишите его в ответ. Если уравнение имеет несколько корней, запишите в ответ их произведение.
Решение: Начинаем анализ с ОДЗ корней:
x2-x-6>0;
-2x>0; x<0.
Уравнение под корнем можно записать в виде
(x-3)(x+2).
Окончательно ОДЗ запишем интервалом
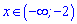 .
.
Возносим обе стороны уравнения к квадрату
x2-x-6=-2x;
x2+x-6=0;
(x+3)(x-2)=0;
x=2; x=-3.
Первый корень не принадлежит ОДЗ, следовательно единственное решение уравнения с корнями x=-3.
Ответ: -3.
Оставайтесь с нами и подготовка к ВНО 2015 по математике останется для Вас приятным воспоминанием и сэкономит много времени и денег на репетиторов. Помощь по математике в виде готовых решений облегчит учебу всех школьников и будет хорошей инструкцией на экзаменах и тестах.


