Логарифмическими называются уравнения содержащие неизвестную величину под знаком логарифма или в основании логарифма (или в обоих местах одновременно). Их легко свести к квадратным или степенным уравнениям относительно переменной если знать свойства логарифма. Например, логарифмическими будут следующие уравнения
Необходимо отметить что во время решения логарифмических уравнений необходимо учитывать область допустимых значений ( ОДЗ ) : под знаком логарифма могут находиться только положительные величины, в основе логарифмов - положительные, отличные от единицы. Однако нахождения ОДЗ порой может быть очень громоздким и на практике имеем возможность или искать ОДЗ, или сделать проверку подстановкой корней уравнения.
Простейшим логарифмическим уравнением называют уравнение вида
Его решение вычисляется потенцированием (нахождение числа или выражения по его логарифму)
В некоторых случаях, решая логарифмические уравнения, целесообразно производить замену переменной. Например в уравнении
удобно сделать замену 
и мы приходим к квадратному уравнению. Причем оба корни этого квадратного уравнения можно подставить в замену чтобы найти подходящее х.
Стоит запомнить что десятичный логарифм от единицы со следующими нулями равно количеству нулей в записи этого числа.
Для десятичного логарифма от единицы с предыдущими нулями правило подобное. Он равен количеству всех нулей в записи этого числа, включая и ноль целых, взятых со знаком минус. Для примера
На этом необходимый теоретический материал рассмотрен и можно переходить к рассмотрению практических примеров. Внимательно рассмотрите их решения это позволит усвоить некоторые правила логарифмов и увеличит практическую базу, которая пригодится при прохождении ВНО , контрольных, тестах и т.д.
Пример 1. Решить уравнение.
Решение. Используя свойство логарифмов переписываем уравнение в виде
Делаем замену
и переписываем
Умножаем на переменную и записываем в виде квадратного уравнения
Вычисляем дискриминант
Корни уравнения приобретут значения
Возвращаемся к замене и находим
Уравнение имеет два решения
Пример 2. Решить уравнение.
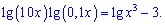
Решение. Раскрываем скобки и записываем в виде суммы логарифмов
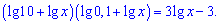
Учитывая что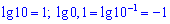 
уравнение примет вид
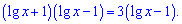
Переносим слагаемое за знаком равенства в правую сторону
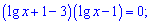
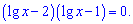
Оба множители приравниваем к нулю и находим
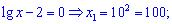
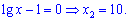
Пример 3. Решить уравнение.
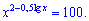
Решение. Перепишем правую сторону в виде квадрата и прологарифмируем по основанию 10 обе части уравнения
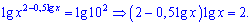
делаем замену
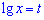
и сводим уравнение к квадратному
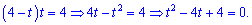
Дискриминант такого уравнения принимает нулевое значение - уравнение имеет два одинаковых решения
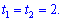
Возвращаемся к замене которую делали выше
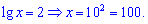
Пример 4. Решить уравнение.
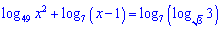
Решение. Выполним некоторые преобразования с слагаемыми уравнения
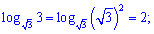
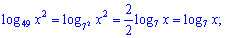
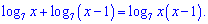
Логарифмическое уравнение упростится до следующего
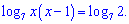
Поскольку логарифмы имеют одинаковые основания то значение под знаком логарифма тоже равны. На основе этого имеем
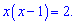
Расписываем и решаем с помощью дискриминанта
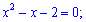
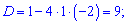
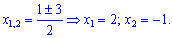
Второй корень не может быть решением, поскольку никакое положительное число при возведены в степени не даст в результате -1. Итак x=2 – единственное решение уравнения.
Пример 5. Найти решение уравнения .
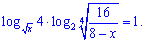
Решение. Выполняем упрощения уравнения
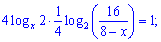
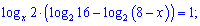
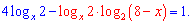
По свойству переходим ко второй основы во втором логарифме
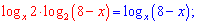
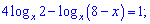
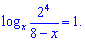
По правилу логарифмирования имеем
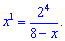
Сводим уравнение к квадратному и решаем его
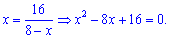
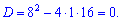
Дискриминант равен нулю, следовательно имеем один корень кратности два
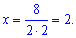
Пример 6. Найти решение уравнения.
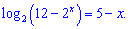
Решение. Заданное уравнение и подобные ему решаются путем сведения к общей основе. Для этого преобразуем правую сторону уравнения к виду
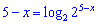
и подставим в уравнение
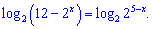
Поскольку основы логарифмов ровны переходим до показательного уравнения
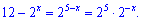
Выполняем замену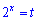 
и сводим к квадратному уравнению
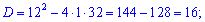
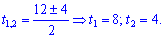
Возвращаемся к замене и вычисляем
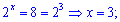
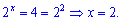
Пример 7. Найти решение уравнения.
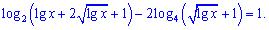
Решение. Не пугайтесь подобных задач, если делать все по правилам то решение получается без труда. Забегая вперед скажу что корни в скобках к примеру отношения не имеют. Они для того чтобы напугать простых математиков.
Упростим сначала второй логарифм
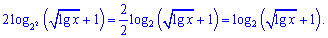
Дальше выполняем подстановку и сведения слагаемых под один логарифм
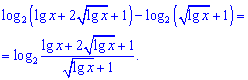
Приравниваем к правой части уравнения и упрощаем
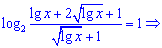
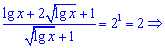
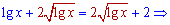
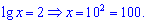
Как видите - решение оказалось проще чем выглядело до решения, а результат x=100 только подтверждает это.
При решении логарифмических уравнений важно хорошо знать свойства логарифмов. Все остальные действия сводятся, как правило, к решению квадратных уравнений или степенных зависимостей относительно неизвестных. Поэтому практикуйте самостоятельно и не имейте проблем с логарифмическими уравнениями.
