Завершением индивидуального задания по теории вероятностей является проверка гипотез. Проверить гипотезу о нормальном распределении генеральной совокупности сможет каждый, кто дочитает статью и будет применять приведенные формулы на практике.
Задания 11 и 12 вариантов помогут в первую очередь экономистам ВУЗов Украины и каждый студент для себя сможет почерпнуть много полезного материала .
Индивидуальное задание 3
Вариант-11
Задача 1. В таблице приведены эмпирические частоты ni и теоретические частоты 
рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости 
0,025 проверить гипотезу H0 про нормальное распределении генеральной совокупности.
Решение: Сначала вычисляем эмпирическое значение критерия Пирсона (m=5)
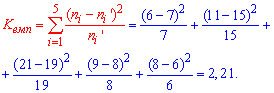
Далее по таблице критических точек распределения хи-квадрат 
для уровня значимости 
0,05 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим (методом интерполяции) критическое значение:
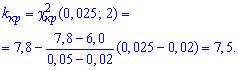
Условие выполняется 
, поэтому гипотезу H0 принимаем.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям 
4,0 получено выборку объемом n=64 и за ней найдено выборочное среднее 
89,7. Для уровня значимости
0,05 проверить гипотезу H0: a=a0=89 при наличии альтернативной гипотезы H1: a>a0.
Решение: Вычислим эмпирическое значение критерия:
Для альтернативной гипотезы H1: a>a0 находим критическое значение uкр по таблице значений функции Лапласа, используя формулы
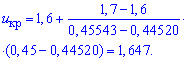
Поскольку условие выполняется 
то гипотезу H0 принимаем.
Задача 3. По выборке объемом n=16 для нормально распределенной генеральной совокупности найдено выборочное среднее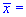 
89,7 и подправленное среднее квадратическое отклонение s=2,0. Для уровня значимости 
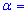0,05 проверить гипотезу a=a0=89 при наличии альтернативной гипотезы H1: a<>a0.
Решение: Вам следует помнить что подправленное и среднее квадратическое отклонение незначительно отличаются на практике. Поэтому формулы которые рассматривали в предыдущем задании актуальны и здесь. Только меняется обозначение с сигма на s. Переходим к нахождению величин, сначала эмпирическое значение критерия:
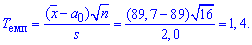
Далее с таблицы критических точек распределения Стьюдента по заданному уровню значимости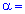 
0,05 (для двусторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку
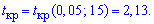
Проверяем условие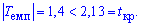 
и принимаем гипотезу H0 .
Как видите вычисления не сложные и по приведенной схеме сможете самостоятельно сделать индивидуальное задания по теории вероятности или контрольную роботу.
Задача 4. Для выборки объемом n=15 нормально распределенной генеральной совокупности найдено подправленную дисперсию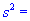 
4,2. Для уровня значимости 
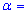0,1 проверить гипотезу 
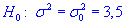при наличии альтернативной гипотезы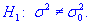 
Решение:
По формуле находим эмпирическое значение критерия Пирсона:
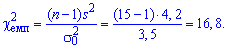
С помощью таблицы критических точек распределения "хи -квадрат"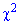 
определяем критические точки слева и справа
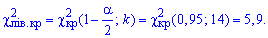
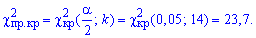
Поскольку эмпирическое значение принадлежит интервалу
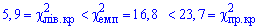
то гипотезу H1 принимаем.
Задача 5. По выборке объемом n=21 нормально распределенной генеральной совокупности найдено подправленную дисперсию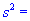 
3,4. Для уровня значимости 
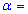0,025 проверить гипотезу 
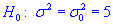при наличии альтернативной гипотезы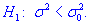
Решение: Определяем эмпирическое значение критерия:
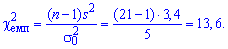
Далее с таблицы критических точек распределения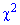 
находим значение
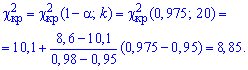
Сравнением величины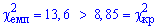 
и делаем вывод о принятии гипотезы H0.
Индивидуальное задание 3
Вариант 12
Задача 1. В таблице приведены эмпирические частоты 
и теоретические частоты 
, рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости 
0,05 проверить гипотезу H0 о нормальном распределении генеральной совокупности.
Решение: Схема расчетов достаточно проста и сводится к нахождению и сравнения двух величин.
Сначала вычисляем эмпирическое значение критерия Пирсона (для m = 5) по формуле
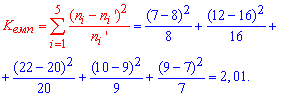
Далее по таблице критических точек распределения "хи-квадрат" 
для уровня значимости 
0,05 и числа степеней свободы 2
(r=2 для нормального распределения) находим критическое значение:
Сравнением емпирическое и критическое значения для гипотезы
и принимаем гипотезу H0.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям
1,75 получено выборку объемом n=49 и за ней найдено выборочное среднее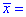 
84,7. Для уровня значимости 
0,1 проверить гипотезу H0: a=a[0]=85 при наличии альтернативной гипотезы H1: a < a[0].
Решение:
Вичысляем эмпирическое значение критерия Пирсона:
Для альтернативной гипотезы H1: a < a[0] находим критическое значение 
по таблице значений функции Лапласа. Для уточнения uкр используем формулу интенрполяции
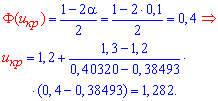
Поскольку выполняется условие 
то принимаем гипотезу H0.
Задача 3. По выборке объемом n=9 нормально распределенной генеральной совокупности найдено выборочное среднее 
84,7 и подправленное среднее квадратическое отклонение s=0,5. Для уровня значимости 
0,01 проверить гипотезу 
при наличии альтернативной гипотезы. 
Решение: Согласно методике вычислим эмпирическое значение критерия:
Далее по таблице критических точек распределения Стьюдента находим для заданного уровня значимости 
0,01 (для двусторонней критической области) и количеством степеней свободы k=9-1=8 критическую точку
.
Сравнением емпирическое и критичное значение 
и приходим к выводу, что гипотезу H0 принимаем.
Задача 4. По выборке объемом n=29 нормально распределенной генеральной совокупности найдено подправленную дисперсию 
7,7. Для уровня значимости 
0,05 проверить гипотезу H0 :
при наличии альтернативной гипотезы H1:
Решение: Вычислим эмпирическое значение критерия по формуле
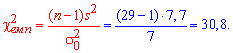
С помощью таблицы критических точек распределения "хи-квадрат" 
определяем «левую» критическую точку
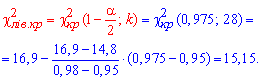
и «правую» критическую точку
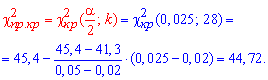
Так как эмпирическое значение принадлежит найденному интервалу
то гипотезу H1 принимаем..
Задача 5. По выборке объемом n=25 нормально распределенной генеральной совокупности найдено подправленную дисперсию 
6,2. Для уровня значимости 
0,05 проверить гипотезу H0:
при наличии альтернативной гипотезы H1 
Решение: Находим эмпирическое значение критерия "хи -квадрат":
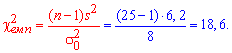
Далее с помощью таблицы критических точек распределения 
определяем
Поскольку условие 
выполняется, то гипотезу H0 принимаем.
Теперь Вы знаете, как проверить гипотезу о нормальном распределении генеральной совокупности.
Готовые решения по теории вероятностей
