Продолжаем разбирать индивидуальное задание по теории вероятностей. Приведенная схема вычислений поможет найти доверительный интервал. Формулы для интервала доверия несложные, в этом Вы скоро убедитесь. Приведенные задачи задавали экономистам ЛНУ им. И.Франка. ВУЗы других городов Украины имеют подобную программу обучения, поэтому для себя часть полезного материала найдет каждый студент.
Индивидуальное задание 1
Вариант 11
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
а) если γ=0,92, генеральная среднее квадратичное отклонение σ=4,0, выборочное среднее  =15,0, а объем выборки n=16;
=15,0, а объем выборки n=16;
б) если γ=0,99, подправленное среднее квадратичное отклонение s=4,0, выборочное среднее ![]() =20,0, а объем выборки n=16.
=20,0, а объем выборки n=16.
Решение: а) Из уравнения ![]()
 с помощью функции Лапласа методом интерполяции находим t
с помощью функции Лапласа методом интерполяции находим t
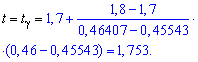
Границы интервала доверия ищем по формулам:
![]()
![]()
После вычислений получим интервал доверия ![]() с надежностью
с надежностью ![]() 0,92.
0,92.
2, б) Поскольку n=16<30 и среднее квадратичное отклонение  неизвестно, то для нахождения границ интервала доверия используем формулу
неизвестно, то для нахождения границ интервала доверия используем формулу
![]()
где ![]() ищем с помощью таблиц (распределение Стьюдента):
ищем с помощью таблиц (распределение Стьюдента):
![]()
![]()
![]()
Таким образом доверительный интервал равный ![]() с надежностью
с надежностью ![]() =0,99.
=0,99.
Задача 3. Найти интервал доверия для оценки с надежностью γ=0,99 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 35, а подправленное среднее квадратичное отклонение s=13,3.
Решение: Задача сводится к отысканию интервала доверия ![]() который покрывает
который покрывает  с заданной надежностью
с заданной надежностью ![]() 0,99.
0,99.
По таблице находим q
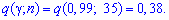
Искомый доверительный интервал лежит в пределах ![]() или
или
![]() .
.
Вариант 1
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
- а) если
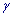 =0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее
=0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее  =7,0, а объем выборки n=9;
=7,0, а объем выборки n=9; - б) если
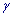 =0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее
=0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее  =15,0, а объем выборки n=9.
=15,0, а объем выборки n=9.
Решение: а) Из уравнения на функцию Лапласа ![]() с помощью таблиц методом интерполяции находим t
с помощью таблиц методом интерполяции находим t
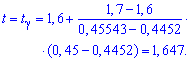
Интерполяцию используем для уточнения t (когда в таблице значений функции Лапласа Ф(t) находится между двумя соседними).
Границы интервала доверия ищем по формулам:
![]()
![]()
Окончательно получаем такой интервал доверия ![]() с надежностью
с надежностью 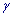 =0,9 2.
=0,9 2.
б) Поскольку n=9<30 и среднее квадратичное отклонение ![]() неизвестно, то для нахождения границ интервала доверия используем формулы
неизвестно, то для нахождения границ интервала доверия используем формулы
![]() ,
,
где значение t ![]() ищем с помощью таблиц распределения Стьюдента:
ищем с помощью таблиц распределения Стьюдента:
![]()
![]()
![]()
Формулы как видите не сложные и найти интервал доверия может как студент, так и школьник.
Мы нашли интервал доверия![]() с надежностью
с надежностью ![]() =0,95.
=0,95.
Задача 3. Найти интервал доверия для оценки с надежностью ![]() =0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
=0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
Решение: Формулы для интервала доверия ![]() достаточно просты.
достаточно просты.
По таблице находим значение функции q
![]()
Далее по формулам вычисляем интервал доверия
![]()
После вычислений он будет лежать в пределах
![]()
Вариант-12
Задача 2. Найти доверительный интервал для оценки с надежностью ![]() неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
а) если ![]() =0,94, генеральная среднее квадратичное отклонение
=0,94, генеральная среднее квадратичное отклонение ![]() =5,0, выборочное среднее
=5,0, выборочное среднее ![]() =18,0, а объем выборки n=25;
=18,0, а объем выборки n=25;
б) если ![]() =0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее
=0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее ![]() =26,0, а объем выборки n=25.
=26,0, а объем выборки n=25.
Решение: а) Из уравнения на функцию Лапласа ![]() с помощью таблиц распределения методом интерполяции находим t
с помощью таблиц распределения методом интерполяции находим t
Крайние точки доверительного интервала ищем по формуле:
![]()
![]()
Итак, интервал принимает множество значений ![]() с надежностью 0,94.
с надежностью 0,94.
2, б) Поскольку n=25<30 и среднее квадратичное отклонение ![]() неизвестно, то для нахождения границ интервала доверия используем формулы
неизвестно, то для нахождения границ интервала доверия используем формулы
![]()
где значение t - ![]() ищем с помощью таблиц распределения Стьюдента:
ищем с помощью таблиц распределения Стьюдента:
![]()
Далее находим границы интервала доверия.
![]()
![]()
Таким образом нашли доверительный интервал ![]() с надежностью
с надежностью ![]() 0,999.
0,999.
Задача 3. Найти доверительный интервал для оценки с надежностью ![]() =0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
=0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
Решение: Найдем интервал доверия по формуле
![]()
По таблице находим значение функции q
![]()
После этого выполняем вычисления границ интервала доверия
![]()
![]()
Как видите формулы для вычисления доверительного интервала не сложные, поэтому с легкостью применяйте их на контрольных и тестах по теории вероятностей.
Готовые решения по теории вероятностей
- Предыдущая статья - Построение уравнения прямой регрессии Y на X
- Следующая статья - Проверка гипотез о нормальном распределении генеральной совокупности


