Рассмотрим пространство элементарных событий, в котором каждому элементарному событию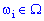 
в соответствие ставится число 
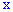или вектор 
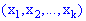, т.е. на множестве 
есть определенная функция 
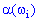, которая для каждого элементарного события 
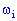находит элемент одномерного пространства 
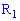или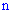 
- мерного пространства 
.
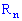Эту функцию называют случайной величиной. В случае, когда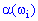 
отражает множество 
на одномерное пространство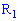 
случайную величину называют одномерной. Если отображение осуществляется на 
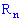, то случайную величину называют n- мерной (системой n случайных величин или n - мерным случайным вектором).
Величина называется случайной, если в результате проведения опыта под влиянием случайных факторов она приобретает то или другое возможное числовое значение с определенной вероятностью.
Если множество возможных значений случайной величины является счетно, то ее называют дискретной. В противном случае ее называют непрерывной.
Случайные величины для удобства обозначают прописными буквами латинского алфавита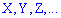 
, а их возможные значения - строчными 
.
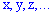Для установления случайной величины необходимо знать не только множество возможных ее значений, но и указать, с какими вероятностями она приобретает то или иное возможное значение.
С этой целью вводят понятие закона распределения вероятностей – зависимость, которая устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины 
часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.
При табличной формы записи закона указывается множество возможных значений случайной величины находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:
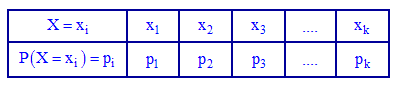
Случайные события должны быть попарно несовместимы и образовывать полную группу, то есть удовлетворять условие:
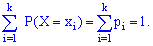
Приведенную зависимость называют условием нормировки для дискретной случайной величины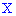 
, а таблицу распределения – рядом распределения.
Функция распределения вероятностей и ее свойства
Закон распределения вероятностей можно представить в виде функции распределения вероятностей случайной величины 
, которая может использоваться как для дискретных, так и для непрерывных случайных величин.
Функцию аргумента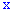 
, устанавливающую вероятность случайного события 
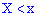называют функцией распределения вероятностей:
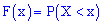
Ее следует понимать как функцию, которая устанавливает вероятность случайной величины, которая может принимать значения, меньше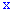 
.
Функция распределения обладает следующими свойствами:
1. Она всегда положительная со значениями в пределах от нуля до единицы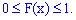 
2. Функция является монотонно возрастающей, а именно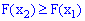 
, если 
.
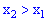С этого свойства получают приведенные выводы:
a) Вероятность вступления случайной величиной возможных значений из промежутка 
равна прироста ее интегральной функции на этом промежутке:
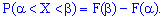
б) Вероятность, что непрерывная случайная величина примет конкретное возможное значение, всегда равна нулю
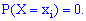
Для непрерывной случайной величины выполняются такие равенства:
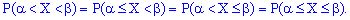
3. На крайних точках непрерывная случайная величина принимает значение 0 и 1.
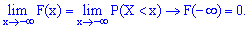
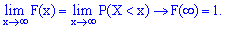
Из этих границ следует, что для дискретной случайной величины с возможными значениями из ограниченного промежутка 
имеем
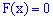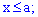
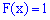для 
для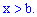 
----------------------------
Приведем решения задач на отыскание функции распределения.
Пример 1. Закон распределения дискретной случайной величины задан таблицей:
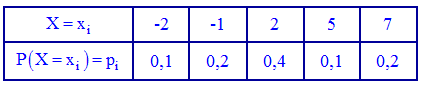
Построить функцию распределения и ее график.
Решение. Согласно свойствами функции получим приведенные дальше значение.
1) 
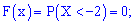
2) 
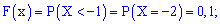
3) 
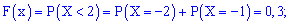
4) 
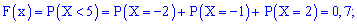
5) 
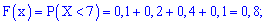
6) 
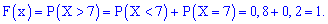
Компактно функция распределения иметь запись
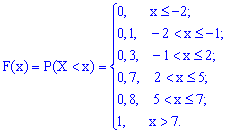
График функции распределения изображен на рисунке ниже
----------------------------
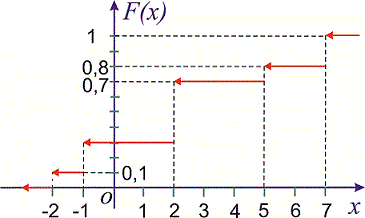
Пример 2. Есть три коробки с шарами. В первой содержится 6 желтых и 4 синие шарики, во втором - 7 желтых и 3 синие, а в третьем - 2 желтых и 8 синих. Из каждой коробки наугад берут по одному шарику. Построить закон распределения вероятностей дискретной случайной величины – появления числа синих шариков среди трех наугад взятых, определить закон распределения и построить график этой функции.
Решение. Среди трех наугад взятых шариков число синих может быть 0, 1, 2, 3.
В табличной форме закон распределения дискретной случайной величины имеет вид:
Вычислим вероятности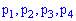 
. С этой целью обозначим 
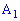- случайное событие, заключающееся соответственно в появлении желтого шарики и 
– появление синего с первой коробки. Подобным образом для остальных коробок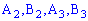 
. Вероятности этих событий такие:
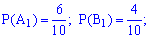
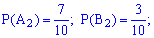
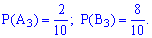
Поскольку случайные события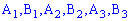 
независимы, то вероятности находим по формулам:
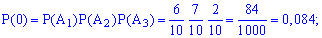
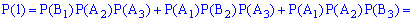
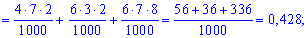
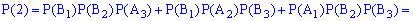
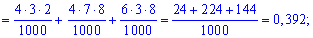
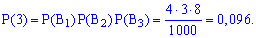
Вычисление достаточно просты и сделаны обозначения полностью все объясняют. Проверим выполнение условия нормировки
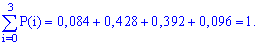
Всегда выполняйте проверку данного условия: это достаточно просто сделать и позволяет быстро проверить правильность вычислений вероятности. В случаях, когда условие нормировки не выполняется нужно отыскать ошибку и исправить ее.
У нас же все вычисления правильны, потому записываем закон распределения вероятностей в табличной форме:
Вычисляем значение интегральной функции
1) 
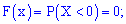
2) 
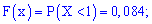
3) 
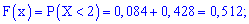
4) 
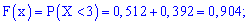
5) 
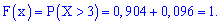
В случае ошибок при нахождении вероятностей последнее соотношение дает отличный от единицы результат, поэтому можете проверять и по этому значению. Упрощенно функция распределения будет иметь вид
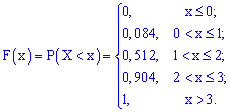
а ее график следующий
----------------------------
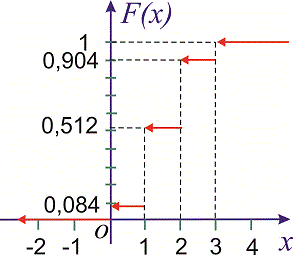
Пример 3. Закон распределения случайной величины 
задан функцией распределения вероятностей
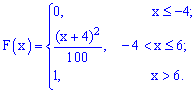
Построить график функции распределения и вычислить вероятность, что случайная величина принадлежит промежутку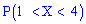 
.
Решение. Функция распределения будет иметь вид.
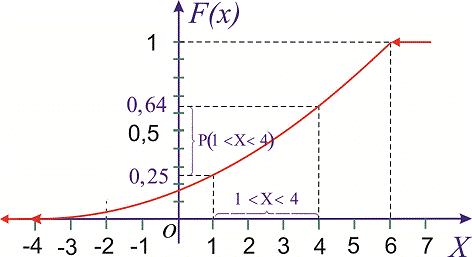
Используя определение, вычислим
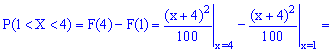
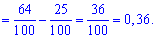
Таким образом вероятность, что случайная величина принадлежит промежутку [1,4] равна 0,36.
----------------------------
Внимательно разберитесь с приведенными примерами нахождения функции распределения, это Вам пригодится на практических занятиях. Старайтесь проверять условие нормирования, чтобы избежать дальнейших ошибок и правильно определяйте вероятности.
----------------------------------------------
