Числовые характеристики статистического распределения

Ответы на индивидуальные задания по теории вероятностей на определение числовых характеристик статистического распределения выборки, нахождение уравнения регрессии между двумя признаками, примеры на проверку гипотезы А при существующей гипотезе В помогут успешно сдать сессию студентам. Все что Вам нужно это внимательно разобраться с методикой нахождения всех возможных характеристик распределений.

Вариант 13. Индивидуальное задание 1.

Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

1. выборочное среднее;
2. выборочную дисперсию;
3. подправленную дисперсию;
4. выборочное среднее квадратичное отклонение;
5. подправленное среднее квадратичное отклонение;
6. размах выборки;
7. медиану;
8. моде;
9. квантильне отклонения;
10. коэффициент вариации;
11. коэффициент асимметрии;
12. эксцесс для выборки:

Задача сформированы в виде таблицы (далее - по вариантам, № варианта = № студента в списке группы)
7, 6, 5, 8, 6, 5, 6, 9, 8, 7, 10, 5, 4, 9, 7, 9, 6, 9, 11, 6.
Решение: Запишем выборку в виде вариационного ряда (в порядке возрастания):
4; 5; 5; 5; 6; 6; 6; 6; 6; 7; 7; 7; 8; 8; 9; 9; 9; 9; 10; 11.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:
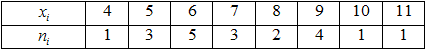Эмпирическую функцию распределения определять по формуле

где n_x количество элементов выборки которые меньше х.
Используя таблицу и учитывая что объем выборки равен

запишем эмпирическую функцию распределения:

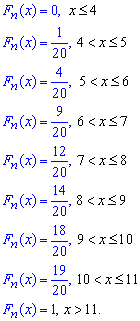
Далее вычисляем числовые характеристики статистического распределения выборки.
1) выборочное среднее находим по формуле

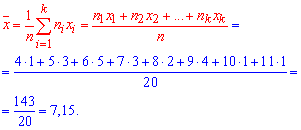
2) выборочную дисперсия вычисляем по формуле



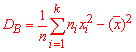
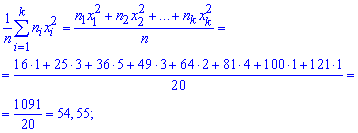
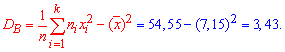
3) подправленную дисперсию находим по формуле

4) выборочное среднее квадратичное отклонение вычисляем по формуле

5) подправленное среднее квадратичное отклонение находим по формуле

6) Размах выборки вычисляем как разность между наибольшим и наименьшим значениями ее вариантов, а именно:

7) Медиану вычисляют согласно формулам:

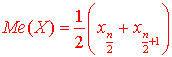
если число n - четное;

если число п - нечетное.
Здесь берем индексы x_i в соответствии с нумерацией вариант в вариационном ряду.
В нашем случае п=20, поэтому

8) Мода - это варианта которая в вариационном ряду случается чаще всего, то есть
9) Квантильное отклонение вычисляют по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем мнимым разбитием вариационного ряда на 4 равные части.
В нашем случае

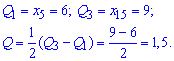
10) Коэффициент вариации находим по формуле

11) Коэффициент асимметрии вычисляем по формуле

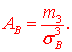
В числителе центральный эмпирический момент 3-го порядка, который находим по формуле

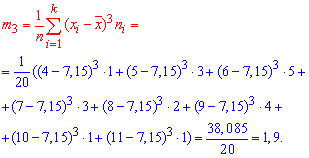
Таким образом коэффициент асимметрии равен 0,3

12) Эксцессом статистического распределения выборки называется число, которое вычисляется по формуле:

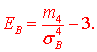
Здесь центральный эмпирический момент 4-го порядка


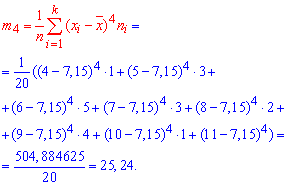
Итак, получим отрицательный эксцесс E_B=-0,85.
На этом индивидуальное задание №1 решено. Из него вы научились находить числовые характеристики дискретного распределения.

Готовые решения по теории вероятностей

• Следующая статья - Уравнение прямой регрессии Y на X. Интервал доверия