Примеры на показательные уравнения и системы уравнений довольно часто трудно вычислить. Все ищут помощи в методичке, интернете, среди знакомых. Ниже приведены схемы решения типичных для практики примеров на показательные уравнения. Их Вы можете встретить на контрольной, тестах, прохождении ВНО по математике. объяснения хорошо расписаны, поэтому разбирайте и выбирайте полезный для себя материал.
Пример 1. Решить уравнение 2^(2x+1)+2^(2x+2)+2^(2x)=28.
Решение: Схема решения подобных показательных примеров следующая:
Выносим множитель в наименьшей степени за скобки
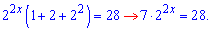
Дальнейшие действия станут ясными в ходе самих вычислений. Как правило, показательные уравнения упрощается до простого типа с которым практически все знают что делать. В нашем случае
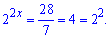
Далее если имеем равные основания (2 = 2) то и показатели должны быть равны 2x = 2; x = 1.
Вот и вся мудрость! Однако на ней можно построить такие показательные уравнения что голова начнет болеть не только у студента, но и у преподавателя которому придется объяснять на доске сложный пример. Поэтому не расслабляйтесь и внимательно посмотрите решения следующих примеров.
Пример 2. Найти произведение решений уравнения 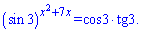
Решение: Такая задача под силу не каждому. Здесь нужно хорошо знать и тригонометрию и показательные уравнения. Преобразуем сначала правую сторону
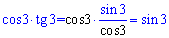
После этого видим, как решить показательное уравнение
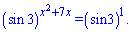
Записано в таком виде, поскольку не все еще научились видеть показатели.
Приравняем их и получим квадратное уравнение
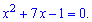
Далее зависит от ваших знаний. Можно решать квадратное уравнение через дискриминант и искать произведение решений уравнения, а можно воспользоваться теоремой Виета что мы и сделаем. Согласно теореме произведение корней равно свободном члену, т.е. (-1).
Вот и все вычисления для данного примера.
Пример 3. Вычислить х+у, если
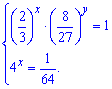
Решение: Имеем систему показательных уравнений с двумя неизвестными. Легкость вычислений заключается в том, что из второго уравнения мы можем найти первую неизвестную и подставить в 1 уравнения. Превратим 2 уравнения к стандартному виду (одинаковому основанию)
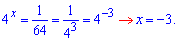
Первая неизвестная равна x=-3. Подставим ее в первое уравнение
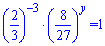
Упростим вторую скобку
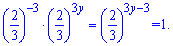
Чтобы число в определенном степени было равное единице необходимо, по свойству показателей, чтобы степень был равен нулю. Решение получим учитывая зависимость
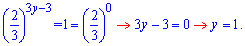
Согласно условия задачи находим сумму корней -3+1=-2.
Пример 4. Найти сумму решений уравнения
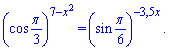
Решение: В основе показательного уравнения имеем тригонометрические функции. Не трудно догадаться, что в подобных примерах они должны принимать одинаковые по модулю значения. Косинус 60 градусе равный синусу 30 i = 1/2.
Иными словами основы равны, осталось приравнять показатели и решить квадратное уравнение.
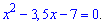
Опять есть два варианта:
- Искать корни через дискриминант и суммировать их.
- Применить теорему Виета.
Согласно теореме сумма корней, взятая с обратным знаком соответствует значению при переменной, т.е.
x1+x2=-(-3,5)=3,5.
Рассмотрим более сложные варианты заданий.
Пример 5. Найти большее решение уравнения
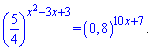
Решение: Перепишем правую сторону показательного уравнения
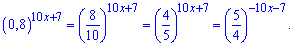
Здесь мы поднесли к (-1) степени основу, соответственно в показателе поменяли знак на противоположный. Приравнивая показатели получим квадратное уравнение
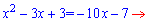
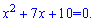
Дискриминант посчитаем в уме (49-40=9). Корень из дискриминанта равен 3.
Больший из корней уравнения принимает значение х=(-7+3)/2=-2.
Пример 6. Найти отрицательное решение уравнения 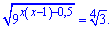
Решение: В первую очередь нужно свести обе стороны показательного уравнения к одной основе. Выполняем преобразования
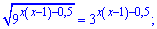
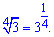
Окончательное уравнение преобразуется к следующему

Приравниваем показатели
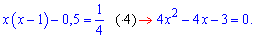
Находим дискриминант квадратного уравнения (16+4*4*3=64) и искомый отрицательный корень
x=(4-8)/(2*4)=-0,5.
Пример 7. Найти натуральный корень уравнения
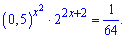
Решение: Сведем показательное уравнение к одному основанию
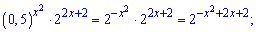
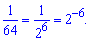
Уравнение упростится к стандартному
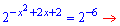
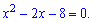
Вычисляем дискриминант
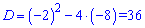
и корни уравнения
x1=(2+6)/2=4;
x2=(2-6)/2=-2 – не является натуральным числом.
Итак, единственная правильный ответ x=4.
Пример 8. Сколько решений имеет уравнение
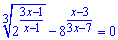 ?
?
Решение: Переносим отрицательное слагаемое за знак равенства и сводим показательное уравнения к общей основе
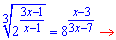
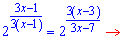
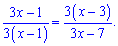
Таким образом показательные уравнение свели к дробному. Прежде всего выписываем ограничения на ОДЗ - исключаем нули знаменателя
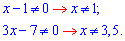
Переходим к перекрестному умножения
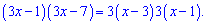
далее раскрываем скобки и группируем подобные слагаемые
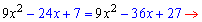
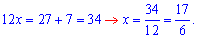
Получили, что уравнение имеет только одно решение x=17/6.
На сайте можете найти много доступных решений которые помогут подготовится к экзаменам, возможно некоторым заменят репетитора. Ищите нужные Вам алгоритмы вычислений, полезные для Вас материалы сайта рекомендуйте одноклассникам и знакомым.
Похожие материалы:


