В предыдущей статье наведены определения наклонных, вертикальных, горизонтальных асимптот. Сейчас же будут приведены примеры нахождения асимптот с применением правила Лопиталя. Его удобно применять при нахождении границ с неопределенностями типа ноль на ноль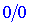 
или бесконечность на бесконечность 
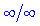, то есть, когда есть границы вида
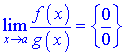
или
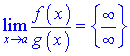
то по правилу Лопиталя ее значение равно
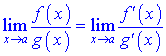
если функции дифференцируемы и определены в окрестности точки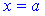 
. Производную можно применять повторно до тех пор, пока не получим константу в числителе или знаменателе или дробь избавится особенности.
------------------------------------
Примеры.
Найти асимптоты функций
І.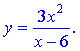 
Решение:
Знаменатель дроби не должен превращаться в ноль
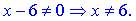
Область определения будет разбита на два интервала
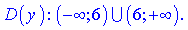
Точка которая разбивает область определения будет вертикальной асимптотой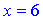 
. Найдем наклонную асимптоту согласно формулы
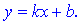
Первую неизвестную найдем с предела
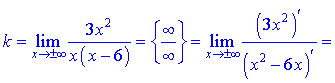
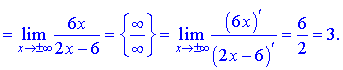
Вторую определяем по правилу
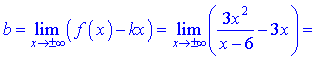
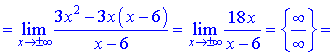
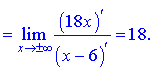
Окончательное уравнение наклонной асимптоты следующее
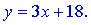
Функцию с асимптотой изображено на графике
------------------------------------------
ІІ.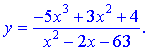 
Решение:
Функция определена во всех точках кроме тех, в которых знаменатель равен нулю. Найдем решения квадратного уравнения
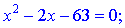
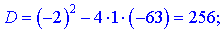
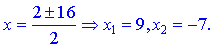
Оба корня разбивают область определения на три интервала
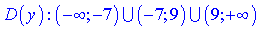
а также являются вертикальными асимптотами функции. Наклонную асимптоту находим с применением правила Лопиталя
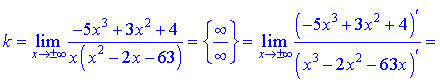
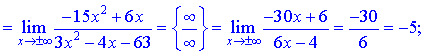
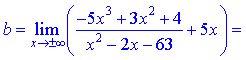
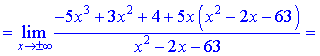
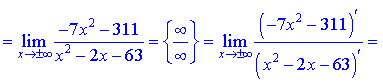
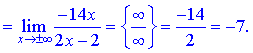
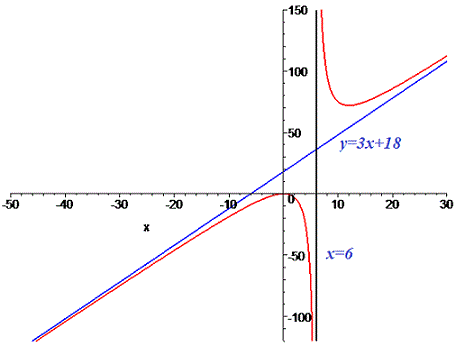
При вычислении констант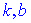 
, входящих в уравнение прямой, пришлось применить правило Лопиталя трижды для первой и дважды для второй неизвестной. В конечном итоге получили следующее уравнение наклонной асимптоты
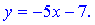
График функции приведен ниже
--------------------------------------
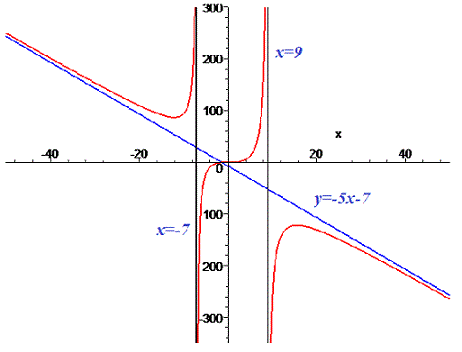
III.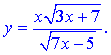 
Решение:
С виду функции следует что она определена во всех точках где определены корни
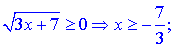
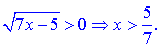
Накладывая оба промежутка получим область определения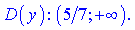 
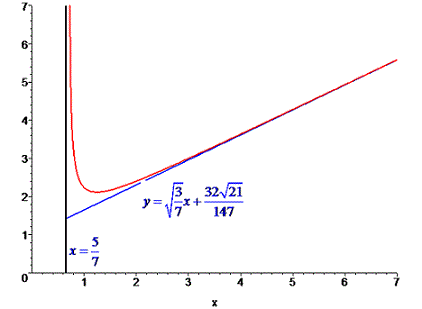
Точка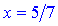 
является вертикальной асимптотой функции. Вычислим коэффициенты, входящие в уравнение наклонной асимптоты. Применение правила Лопиталя к данному примеру никаких упрощений не даст поэтому используем другое
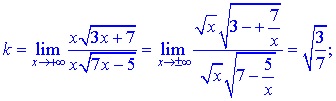
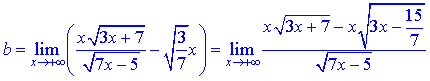
Упростим выражение в числителе
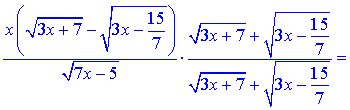
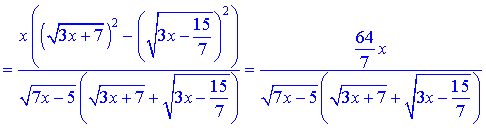
и подставим в границу
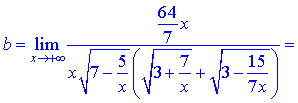
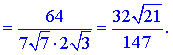
Уравнение наклонной асимптоты примет вид
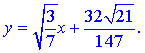
График заданной функции с наклонной асимптотой следующий
--------------------------------------
Приведенные решения частично ознакомили Вас с возможными примерами которые могут быть на практике. Для лучшего владения данной тематикой решайте задачи самостоятельно, изучайте удобные методики нахождения пределов функции которые позволят получить результаты быстрее.
-----------------------------------
Посмотреть материалы:
