Локальный экстремум функции. Примеры

Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.

Точка 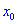называется точкой локального максимума (или минимума) функции 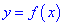, сли существует такой окрестность 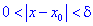этой точки, принадлежащий области определения функции, и для всех 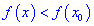из этого окрестности выполняется неравенство 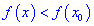(или ).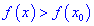

Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках - ее экстремальными значениями.

НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:

Если функция имеет в точке 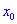локальный экстремум, то либо производная равна нулю 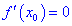, либо не существует.

Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.

Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.

ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ

Теорема І. Пусть функция 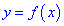непрерывна в некотором интервале, содержащем критическую точку 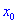и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).

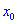Тогда для точки 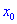функция имеет максимум, если для аргументов 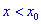выполняется условие, что производная больше нуля 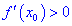, а для 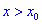условие - производная меньше нуля .

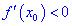Если же для 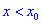производная меньше нуля 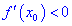, а для 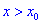больше нуля 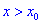, то для точки 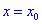функция имеет минимум.

Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки 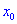и производная равна нулю 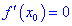. Тогда в точке 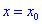функция имеет локальный максимум, если вторая производная меньше нуля 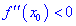и локальный минимум, если наоборот .

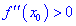Если же вторая производная равна нулю 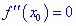, то точка 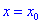может и не быть точкой экстремума.

При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.

ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ

1) найти область определения ;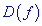

2) найти первую производную ;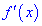

3) найти критические точки;

4) исследовать знак производной 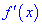на интервалах, которые получили от разбиения критическими точками области определения .

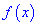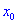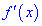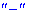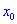При этом критическая точка является точкой минимума, если при переходе через нее слева направо производная меняет знак с отрицательного на положительный , в противном случаэ является точкой максимума.

Вместо данного правила можно определять вторую производную 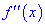и исследовать согласно второй теоремы.

5) вычислить значения функции в точках экстремума.

Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.

-----------------------------------

Примеры.

Сборник В.Ю. Клепко, В.Л. Голец "Высшая математика в примерах и задачах"

1. (4.53.7)

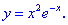
1) Областью определения будет множество действительных чисел

;

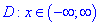2) Находим производную

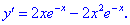
3) Вычисляем критические точки

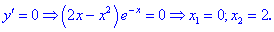
Они разбивают область определения на следующие интервалы

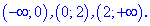
4) Исследуем знак производной на найденных интервалах методом подстановки значений

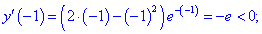
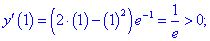
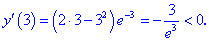
Таким образом первая точка 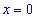является точкой минимума, а вторая 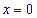- точкой максимума.

5) Вычисляем значение функции

------------------------------

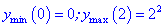
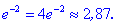
2. (4.53.9)

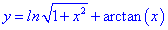
1) Областью определения будет множество действительных чисел , так корень всегда больше единицы

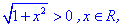
и функция арктангенс определена на всей действительной оси.

2) Находим производную

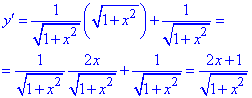
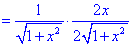
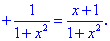
3) С условия равенства производной нулю находим критическую точку

Она разбивает область определения на два интервала

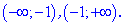
4) Определим знак производной в каждой из областей

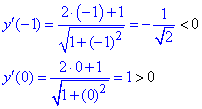
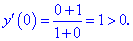
Таким образом находим, что в критической точке 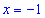функция принимает минимальное значение.

5) Вычислим экстремум функции

------------------------------

3. (4.53.13)

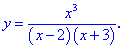
1) Функция определена когда знаменатель не превращается в ноль

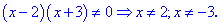
Из этого следует, что область определения состоит из трех интервалов

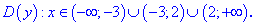
2) Вычисляем производную

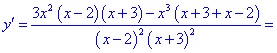
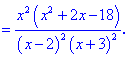
3) Приравниваем производную к нулю и находим критические точки.

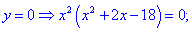
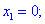
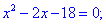
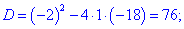
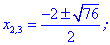
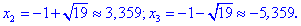
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.

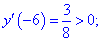
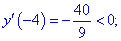
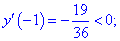
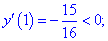
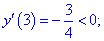
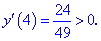
Таким образом точка 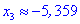является точкой локального максимума, а 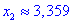локального минимума. В 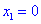имеем перегиб функции, но о нем будет больше материала в следующих статьях.

5) Находим значение в критических точках

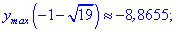
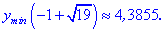
Несмотря на то, что значение функции 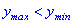, первая точка является точкой локального максимума, а дуга - минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.