Формула Грина. Переход от криволинейного интеграла к двойному

При решении примеров на интегрирование есть ряд заданий где необходимо перейти от криволинейного интеграла к двойному интегралу и наоборот. Формула Грина устанавливает связь между этими интегралами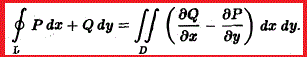

Она справедлива для любой конечной замкнутой области, которую можно разбить на конечное количество правильных для интегрирования областей.
Как это делать на практике раскроем в следующих примерах.

Пример 1 Используя формулу Грина, вычислить криволинейный интеграл:

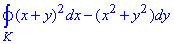
где K - треугольник ABC с вершинами A(1,1), B(3,2), C(2,5).
Решение: Складываем уравнения сторон треугольника ABC:

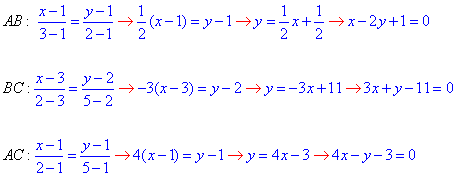
Уравнения нужны для определения точек пересечения прямых и разделения области интегрирования на подобласти.
Треугольник в декартовой плоскости имеет вид

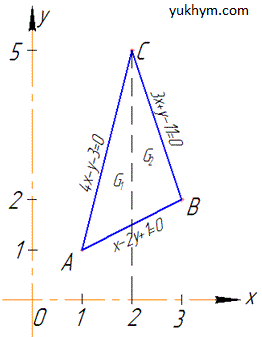
Запишем подынтегральное выражение:
(x+y)²dx-(x²+y²) dy.
Здесь обозначим P=P(x, y)= (x+y)², Q=Q(x, y)=- (x²+y²).
Найдем частичные производные первого порядка функций P, Q:

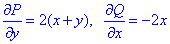
затем их разницу

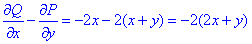
Расставим пределы интегрирования в области G, для этого разделим ее (см. рисунок выше) на две части G=G1+G2, то есть
G1: 1≤x≤2, x/2+1/2≤y≤4x-3;
G2: 2≤x≤3, x/2+1/2≤y≤-3x+11.
Внимательно посмотрите как выполняется интегрирование, помните - определение пределов в интеграле ответственное занятие, ведь от них также зависит правильность результата.
Вычислим криволинейный интеграл, используя формулу Грина: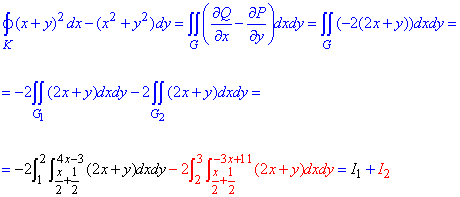

Здесь трудно вместить все в одну формулу, да и Вам трудно будет ее проследить, поэтому каждый из интегралов разберем отдельно

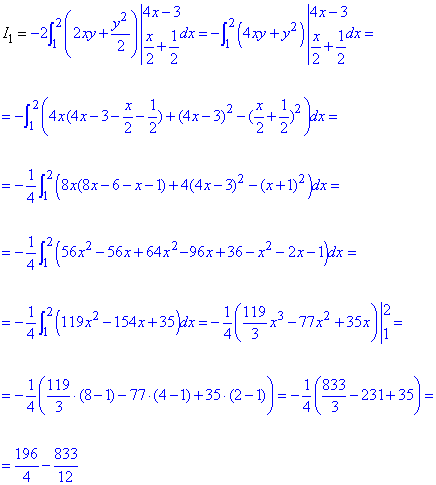
Учитывая что пределы первого интеграла, что берем, являются функциями, придется группировать и упрощать полученные подынтегральные функции.
Подобные манипуляции выполняем со вторым интегралом

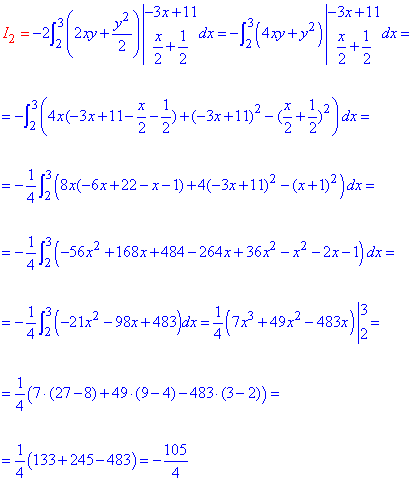
Не забываем напоследок вычислить сумму интегралов

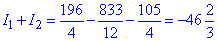
Пример 2 Используя формулу Грина, вычислить криволинейный интеграл:

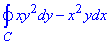
где C - круг x²+y²=a².

Решение: Построим круг вдоль дуги которого будем искать интеграл

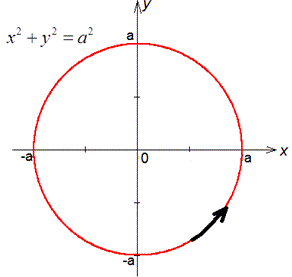
Выпишем подынтегральные функции Q=Q(x, y)=xy² и P=P(x, y)=-x²y.
Найдем частичные производные первого порядка от функций Q, P:

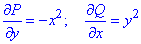
Пределы области интегрирования:
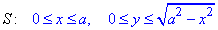 (четверть круга).
Вычислим криволинейный интеграл по формуле Грина :
при интегрировании выполняем переход к полярной системе координат, перечисляем пределы интегрирования и не забываем умножить на якобиан I=r.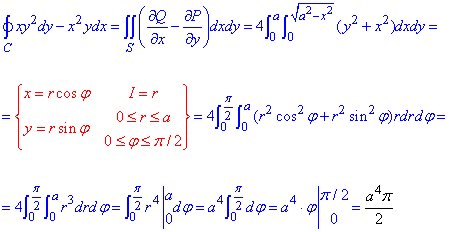

Внимательно разберите как расставлять пределы в кратных интегралах, какие методы и когда позволяют упростить интегрирование.
В будущем статью дополним новыми примерами, но для этого нужны заказы от Вас на расчет такого сорта интегралов.