Поверхностные интегралы ІІ рода

Вычисления поверхностного интеграла второго рода заключается в нахождении двойных интегралов по ориентированным поверхностям от заранее заданных функций. Теория двойных интегралов детально расписана в учебниках и методичках, больше трудностей возникает у студентов с самим интегрированием, вернее с переходом к двойным интегралам, правильным нахождением пределов интегрирования. 
На эти вопросы Вы можете найти ответы, пересмотрев готовые ответы к практикуму из высшей математики.

Пример 6.2 Вычислить поверхностный интеграл int(x*dy*dz+y*dx*dz+z*dx*dy, ds) по поверхности сигма - внешняя сторона куба, ограниченного плоскостями z=0, y=0, x=0, x=1, y=1, z=1.

Решение: Построим куб, который ограничен заданными плоскостями:

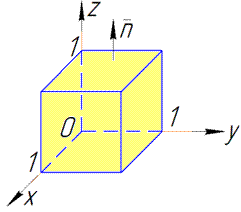
Вычисляем поверхностный интеграл ІІ рода по всем шести поверхностям, поэтому формула примет вид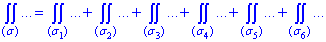

Для каждой поверхности куба запишем уравнение плоскости и ее предела по граням:
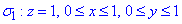отсюда 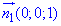- нормальный внешний вектор.
На плоскости Oxz и Oyz поверхность z=1 проектируется в прямые, где dydz=0, dxdz=0

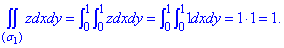
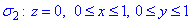отсюда вектор нормали равен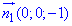
На плоскости Oxz и Oyz поверхность z=0 проектируется в прямые, где dydz=0.

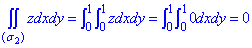
Поскольку в условии куб ограничен плоскостями z=0, y=0, x=0, x=1, y=1, z=1, то по соответствующим плоскостям ситуация будет аналогична, поэтому поверхностный интеграл равен сумме

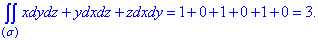
Пример 6.4 Вычислить поток векторного поля 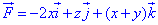через замкнутую поверхность :

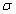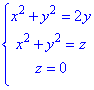
(нормаль внешня).
Решение: Уравнение x^2+y^2=2y сводим к каноническому виду x^2+(y-1)^2=1 - цилиндр вытянут вдоль оси Oz и радиусом R=1;
z=x^2+y^2 - эллиптический параболоид с вершиной в начале координат (0;0;0) ветками вытянут вверх вдоль оси Oz.
Построим цилиндр и параболоид

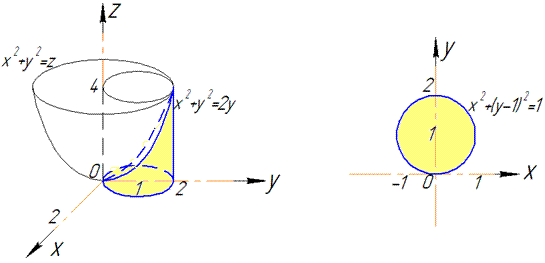
Это вносит определенную ясность в условие задания да и Вам более приятно читать ответы с рисунками, чем голые формулы.
Как видим из рисунка половина области V задается следующими пределами:

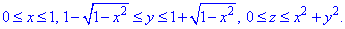
Рассматриваем половины в силу четности всех функций, поэтому конечный результат умножим на 2.
Вычислим дивергенцию векторного поля :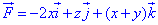

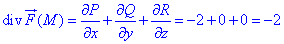
где P=P(x;y;z)=-2x, Q=Q(x;y;z)=z, R=R(x;y;z)=x+y множители при направляющих векторного поля.
Найдем поток векторного поля по формуле Остроградського-Гаусса: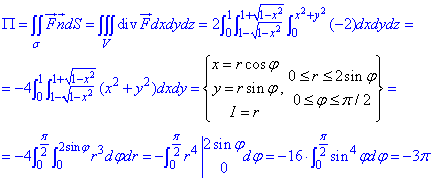

Тройной интеграл сводим к двойному, а дальнейше, перейдя к полярной системе координат, находим значение интеграла.

Пример 6.6 Вычислить поверхностный интеграл int(z²*dy*dz, ds) по поверхности сигма, где - внешняя часть эллипсоида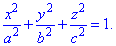

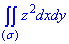
Решение: Построим эллипсоид и его проекцию в декартовую плоскость:

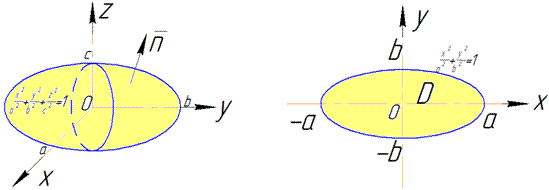
Проекция плоскости на Oxy ограничена следующим образом

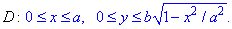
(Взяли четверть области).

Дальше выражаем поверхность как функцию z(x, y)

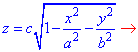
z^2=(1-x^2/a^2-y^2/b^2) *c^2
затем находим дифференциал поверхности по формуле

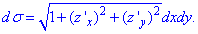
Этот интеграл будем вычислять для верхней половины эллипсоида, поскольку для нижней значение поверхностного интеграла будет таким же. Таким образом, результат умножим на 2.
Вычислим направляющие косинусы поверхности:

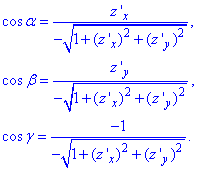
Перед радикалами поставим знак " - ", поскольку внешняя нормаль 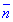 образует с-осью Oz острый угол.
Следовательно, сводим поверхностный интеграл к повторному, дальше делаем замену переменных и находим якобиан перехода.

Все превращения дают возможность без вычисления тяжелых интегралов найти компактный ответ.

Пример 6.9 Вычислить поверхностный интеграл int((y-z)*dy*dz, ds) по поверхности сигма, где сигма - внешняя сторона конической поверхности x^2+y^2=z^2 ().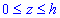

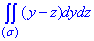
Решение: Построим конус, который ограничен сверху:
x^2+y^2=z^2 ().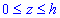

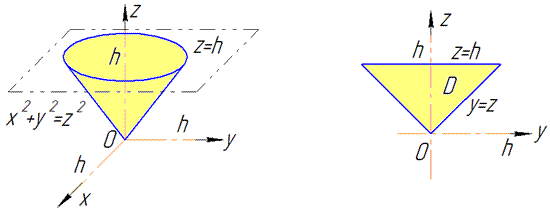
Его проекция в плоскость Oyz дает равнобедренный треугольник, ограниченный линиями

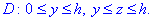
При расстановке пределов учли четность функций, поэтому результат нужно будет умножить на 2.
Находим поверхностный интеграл ІІ рода :

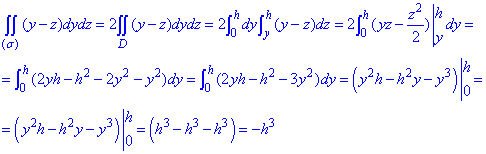
Проинтегрировать приведенные функции по силам каждому студенту.

Пример 6.13 Вычислить поверхностный интеграл int(x*dx*dz, ds) по поверхности сигма, где сигма - внешняя сторона треугольника, образованного пересечением плоскости x-y+z=1 с координатными осями.

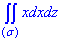
Решение: Построим пространственный треугольник x-y+z=1 и его проекцию.

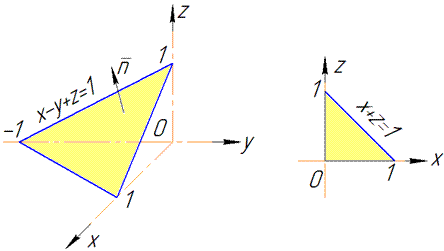
Проектировать всегда следует в ту плоскость Oxz по которой идет интегрирование

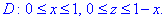
Вычисляем поверхностный интеграл ІІ рода:

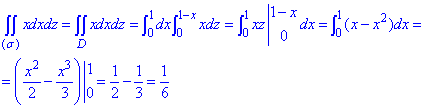
Пример 6.15 Вычислить поверхностный интеграл int(yz*dy*dz, ds) по поверхности сигма - внешняя сторона треугольника, образованного пересечением плоскости x+y+z=4 с координатными осями.

Решение: Построим плоскость сигма: x+y+z=4.

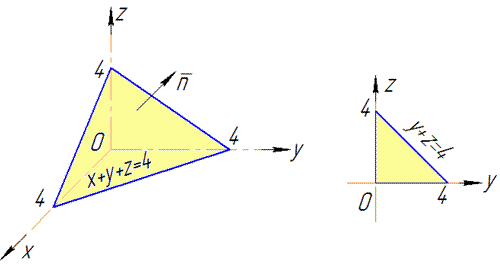
Видим, что проекция треугольника в Oyz имеет такие пределы

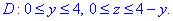
Поверхностный интеграл ІІ рода сводим к повторному и вычисляем

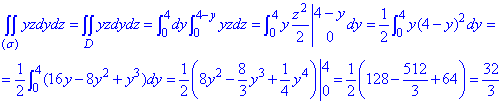
Брать подобные интегралы не сложно, вся проблема сводится к правильному построению поверхности и корректной расстановки пределов интегрирования.
Интегрировать не трудно, поскольку, как правило, заданы самые простые функции.

Пример 6.16 Вычислить поверхностный интеграл int(xz*dx*dz, ds) по поверхности сигма- внешняя сторона треугольника, образованного пересечением плоскости x+y+z=3 с координатными осями.

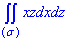
Решение: Построим пространственный треугольник: x+y+z=3.

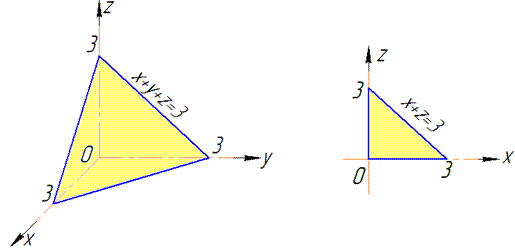
Заданная плоскость проектируется на область D в Oxz следующим образом

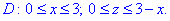
Имея пределы сводим поверхностный интеграл ІІ рода к повторному

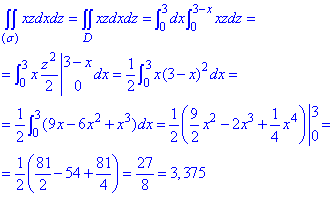
Пример 6.23 Вычислить поверхностный интеграл int((x+z)*dy*dz, ds) по поверхности 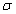, где 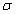- внешняя сторона пирамиды, ограниченной плоскостями x=0, y=0, z=0, x+y+z=1.

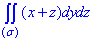
Решение: Выполняем рисунок к задаче

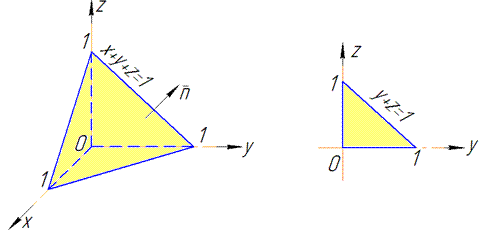
Плоскость проектируется треугольником в Oyz

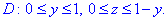
Поверхностный интеграл ІІ рода вычисляем с учетом уравнения поверхности x=1-y-z.

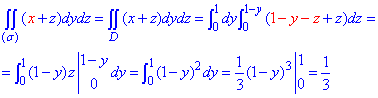
Вычисления сами по себе тяжелые, потому на практических и экзаменах эта тема не должна создавать Вам трудностей.